Malditas proporciones pequeñas I

Cuando uno está en esto de ganarse la vida mediante la ciencia de datos, se da cuenta de que la vida no es tan maravillosa como lo cuentan los libros de texto ni los cursos de los másters y ni siquiera los concursos de kaggle.

Recientemente en un proyecto nos piden detectar un efecto de un incremento del 15% en una proporción entre dos grupos, digamos en forma canónica, grupo de control y tratamiento. Hasta aquí todo normal y uno podría hacer calcular intervalos de confianza (o de credibilidad si nos vamos al mundo bayesiano) de manera más o menos fácil. Veamos como sería utilizando simulación.

Supongamos una p1 = 0.5 y una p2 = p1 * 1.16 ( un pelín superior al 15%) Supongamos también que nuestros grupos tienen tamaño n1 = n2 = 100000. Así que vamos a calcular mediante simulación la probabilidad que p2/p1 >= 1.15. ¿Fácil, verdad?

p1 y p2 los simulamos suponiendo una distribución beta. Supongamos que p2 es un 16% mayor que p1

set.seed(-1) # prueba a poner una semilla negativa en python a ver que pasa
p1 <- 0.5
p2 <- p1 * 1.16
n <- 1E5
sim <- 1E6

sim_beta1 <- rbeta(sim, p1 * n, n - p1 * n)
sim_beta2 <- rbeta(sim, p2*n, n - p2 * n)

median(sim_beta1)
#> [1] 0.5000039
median(sim_beta2)
#> [1] 0.5800018

Si dibujamos sus funciones de densidad con R base sin muchas zirigoncias.

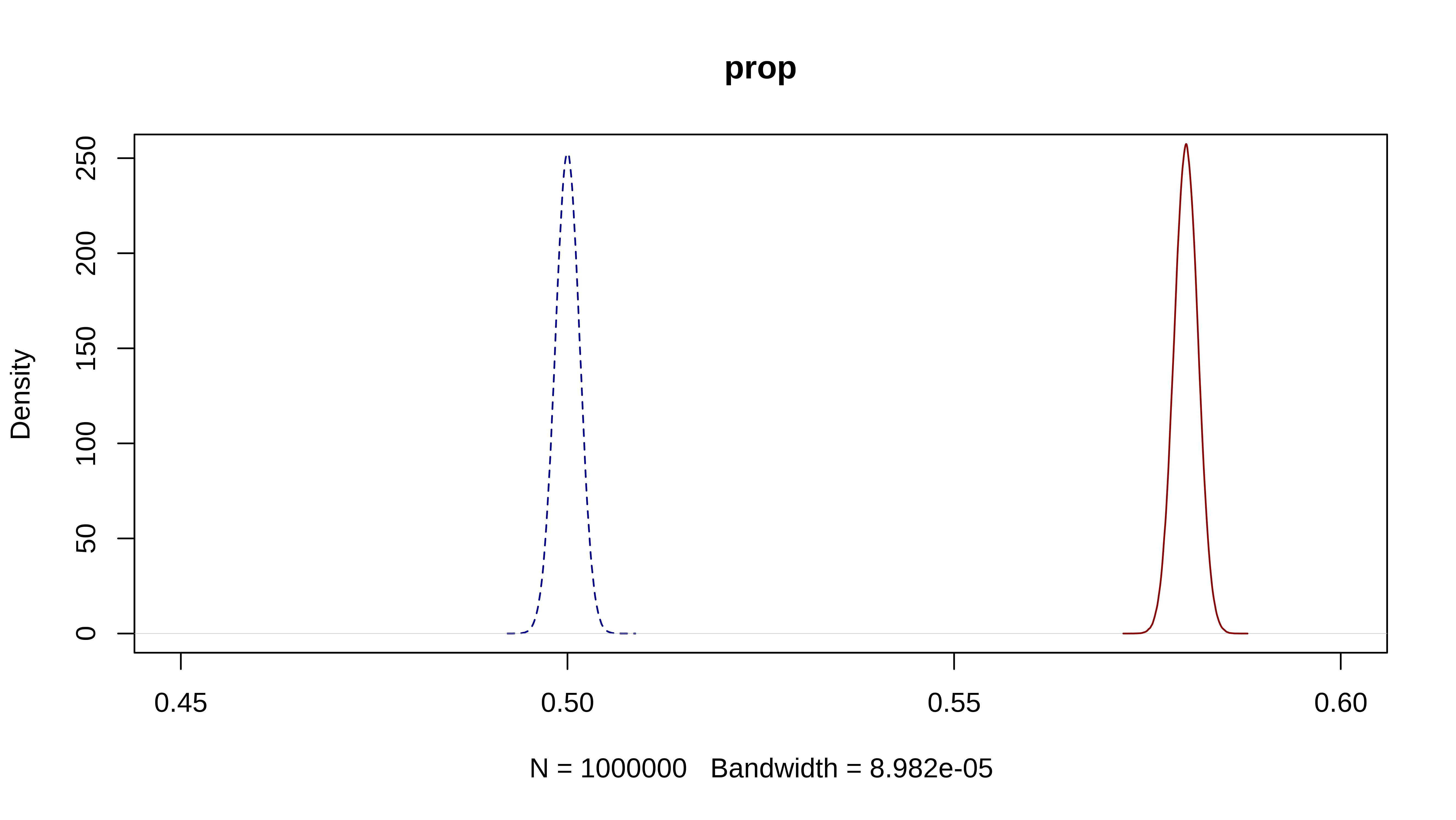
plot(density(sim_beta1), main = "prop", col = "darkblue", lty = 2, xlim = c(0.45, 0.6))

lines(density(sim_beta2), col = "darkred")

Y claramente si que parece que están separadas. Podemos estimar la probabilidad de que p2 sea un 15% mayor como la proporción de veces que p2/p1 >= 1.15 en el millón de simulaciones

mean(sim_beta2/sim_beta1 >= 1.15)
#> [1] 0.98152

Y podríamos estar bastante seguros de que p2 es al menos un 15% mayor que p1.

Pero ¿qué pasa si las proporciones son pequeñas, digamos de un 4 por mil?

set.seed(-1)
p1 <- 0.004
p2 <- p1 * 1.16
n <- 1E5
sim <- 1E6

sim_beta1 <- rbeta(sim, p1 * n, n - p1 * n)
sim_beta2 <- rbeta(sim, p2*n, n - p2 * n)

median(sim_beta1)
#> [1] 0.003997118
median(sim_beta2)
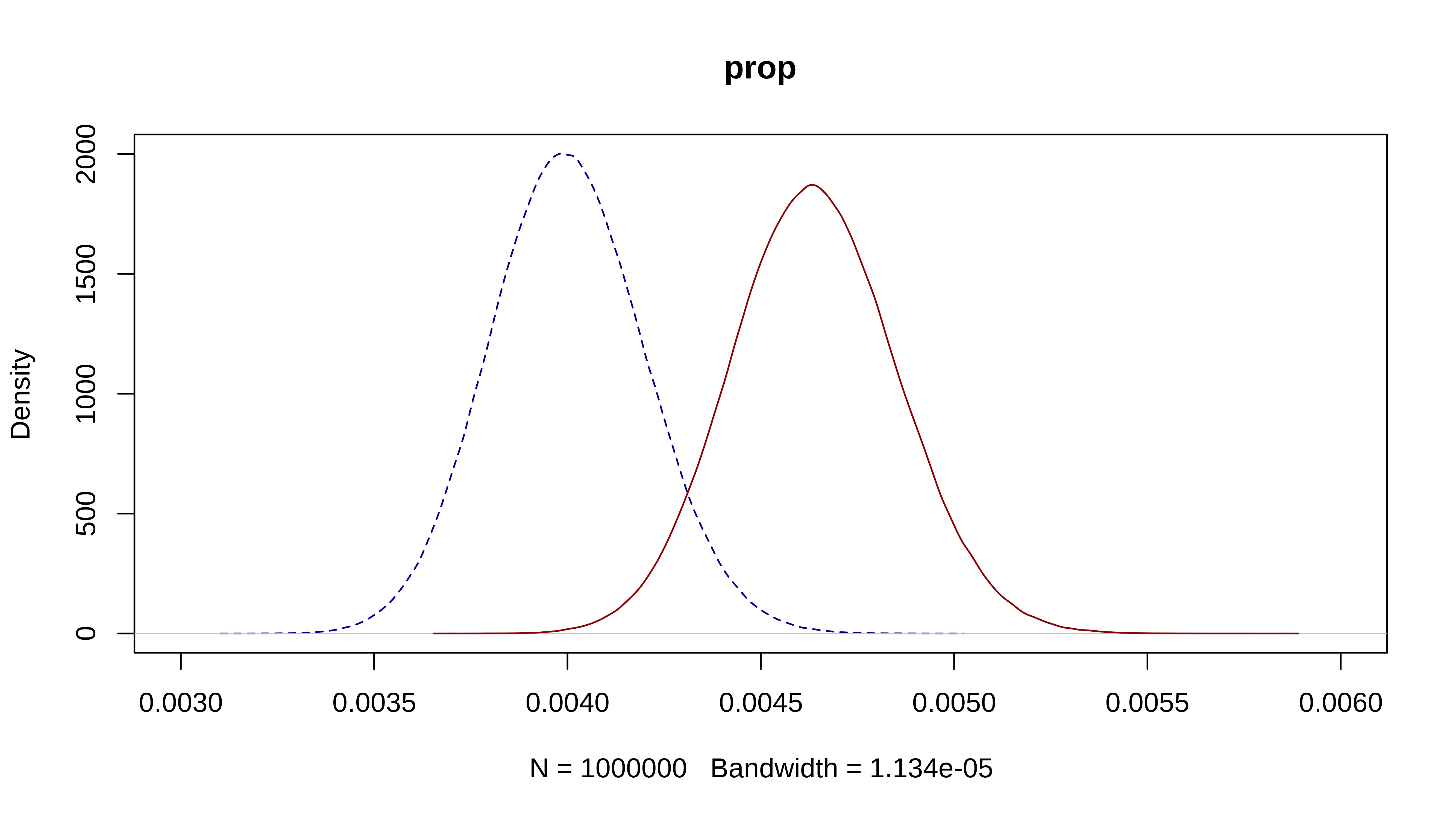
#> [1] 0.004636583

plot(density(sim_beta1), main = "prop", col = "darkblue", lty=2, xlim = c(0.003, 0.006)  )

lines(density(sim_beta2), col = "darkred")

mean(sim_beta2/sim_beta1 >= 1.15)
#> [1] 0.550476

Pues ya no podemos estar tan seguros de que el incremento haya sido de alrededor un 15%.

En próximas entradas veremos como calcular de forma clásica el tamaño muestral necesario para detectar ese efecto.