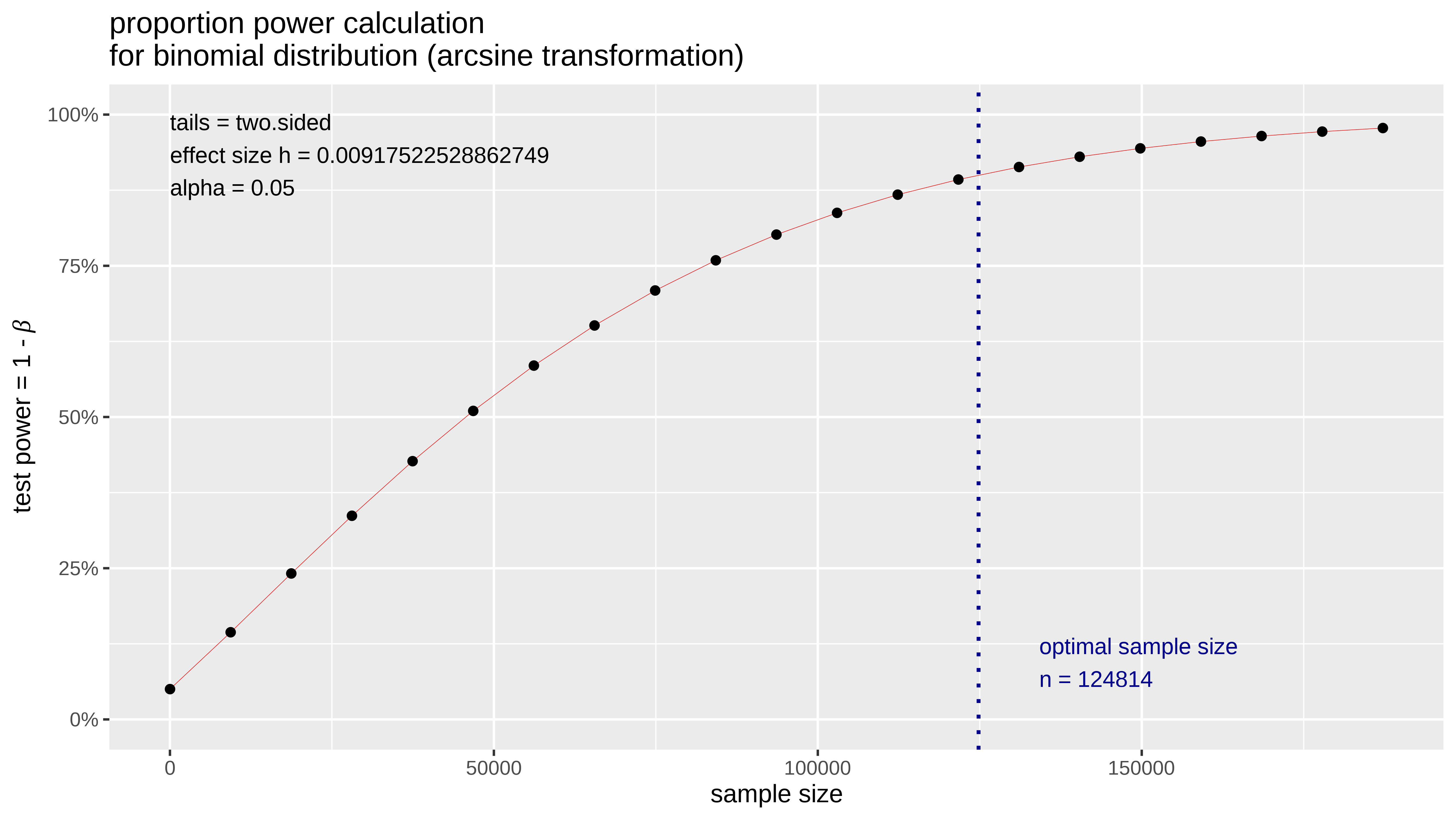
Malditas proporciones pequeñas II

¿Cuál sería el tamaño muestral mínimo para estimar un incremento del 15% en una proporción de digamos 0.004?

En realidad me gustaría hacer como cuenta mi amigo Carlos en este post, pero no puedo ir examinando unidades y actualizar los intervalos de credibilidad hasta que la anchura me convenza, porque ni siquiera conozco al tío de la furgoneta que ha de ir “examinando” cada unidad experimental, amén de que para conseguir 4 tiene que examinar cerca de 1000. Así que veamos como se ha hecho toda la vida.

Nos interesa es minimizar los errore tipo I y tipo II. Recordemos lo que eran.

• Error tipo I : Error de falso positivo, decir que hay diferencias cuando en realidad no las hay (H0 es cierta pero digo que no)
• Error tipo II: Error falso negativo, error que cometo al decir que no hay diferencias cuando en realidad si las hay. (H0 es falsa pero decimos que es verdadera) 8

Si utilizamos el paquete de R pwr podemos calcularlo para un error tipo I, (el alpha de siempre) de 0.05 y una potencia (1 - error tipo II) de 0.9

p1 <- 0.004
p2 <- p1 * 1.15
library(pwr)

potencia_0.9 <- pwr.p.test(ES.h(p1=p1, p2= p2),
                           sig.level= 0.05, power = 0.9) 
plot(potencia_0.9)

Y nos sale que el tamaño de muestra mínimo está en torno a 125 mil .

Hay otras librerías para calcular dicho tamaño muestral, por ejemplo SampleSizeProportions que según pone en la documentación lo hace teniendo en cuenta el intervalo de credibilidad deseado. Tengo que mirar mejor esta librería.

library(SampleSizeProportions)

len <-  (p1 * 1.15 - p1/1.15)
c1 <- 40
c2 <- 46
d1 <- 9960
d2 <- 9954

propdiff.modwoc(len = len, c1 = c1, d1 = d1, c2 = c2, d2 = d2)
#> [1] 120910 120910

Y sale unos 120 mil para cada grupo.

O también podemos ver cosas como está que comentan los amigos de WinVector, aquí o aquí

estimateT <- function(lowProb,difference,errorProb) {
  -log(errorProb/2)*lowProb/(difference^2)
}

# detectar diferencias de 15%
lowProb <- 0.004
incremento <- 0.15
estimateT(lowProb, lowProb*incremento,  0.0006 )
#> [1] 90130.31

Y nos sale un tamaño aproximado de 90 mil. Sea como fuere el tener que determinar tamaños de muestra para poder medir variaciones de un 15% en proporciones pequeñas implica tener muestras de tamaño 100000, así que como dice el título, ¡malditas proporciones pequeñas!