Análisis de correspondencias “old_style”
Quién me conoce sabe que siento debilidad por el análisis de datos categóricos, en particular por técnicas como el análisis de correspondencias simple o múltiple o por las cosas más modernas que hay. No en vano se me dió especialmente bien en la universidad, en parte debido a que por fin me centré después de unos años locos, y en parte debido a algún buen profesor. El caso es que en el curro utilizamos este tipo de técnicas para encontrar relaciones entre variables categóricas que quizá hayan pasado desapercibidas en un primer análisis.
Antes de nada voy a dar un par de referencias en castellano, bastante útiles.
- La práctica del análisis de correspondencias. Michael Greenacre
- Análisis de datos multivariantes. Daniel Peña
De hecho el ejemplo que voy a contar y la notación que voy a usar viene en el libro de Daniel. Es un ejemplo de Fisher (si, ese al que todo el mundo odia hoy en día) de 1940, sobre la relación entre el color de los ojos (en filas) y el color del pelo (en columnas). Se trata de una simple tabla de contingencia.
df <- read.csv("hair_eyes_color.csv")
rownames(df) <- df$color_ojos
df_tabla <- as.matrix(df[,-1])
df_tabla
#> rubio pelirrojo castaño oscuro negro
#> claros 688 116 584 188 4
#> azules 326 38 241 110 3
#> castaños 343 84 909 412 26
#> oscuros 98 48 403 618 85Cuyos totales por filas y columnas son
addmargins(df_tabla)
#> rubio pelirrojo castaño oscuro negro Sum
#> claros 688 116 584 188 4 1580
#> azules 326 38 241 110 3 718
#> castaños 343 84 909 412 26 1774
#> oscuros 98 48 403 618 85 1252
#> Sum 1455 286 2137 1328 118 5324Proyección de las filas.
Podríamos plantearnos la relación entre las filas (color de ojos) , ¿cómo de similares son los que tienen los ojos claros con los que tienen los ojos azules, respecto a su color del pelo?
Parece claro que deberíamos centrarnos en los porcentajes por filas (perfiles fila)
prop.table(df_tabla, 1)
#> rubio pelirrojo castaño oscuro negro
#> claros 0.43544304 0.07341772 0.3696203 0.1189873 0.002531646
#> azules 0.45403900 0.05292479 0.3356546 0.1532033 0.004178273
#> castaños 0.19334837 0.04735062 0.5124014 0.2322435 0.014656144
#> oscuros 0.07827476 0.03833866 0.3218850 0.4936102 0.067891374A partir de ahora vamos a usar la tabla de frecuencias relativas, cuyos elementos llamaremos \(f_{ij}\)
(tabla_frecuencias <- prop.table(df_tabla))
#> rubio pelirrojo castaño oscuro negro
#> claros 0.12922615 0.021788129 0.10969196 0.03531180 0.0007513148
#> azules 0.06123216 0.007137491 0.04526672 0.02066116 0.0005634861
#> castaños 0.06442524 0.015777611 0.17073629 0.07738542 0.0048835462
#> oscuros 0.01840721 0.009015778 0.07569497 0.11607814 0.0159654395Que tiene los mismos porcentajes por filas.
(perfiles_fila <- prop.table(tabla_frecuencias, 1))
#> rubio pelirrojo castaño oscuro negro
#> claros 0.43544304 0.07341772 0.3696203 0.1189873 0.002531646
#> azules 0.45403900 0.05292479 0.3356546 0.1532033 0.004178273
#> castaños 0.19334837 0.04735062 0.5124014 0.2322435 0.014656144
#> oscuros 0.07827476 0.03833866 0.3218850 0.4936102 0.067891374Se podría considerar utilizar la distancia euclídea para ver como de parecidas son las filas ojos claros y ojos azules, pero eso presenta un problema, que es la distribución del color del pelo en la tabla, dónde por ejemplo el porcentaje de rubios es mayor que el de pelirrojos. Así que usar esa distancia no sería justo. Podríamos definir una distancia ponderada que fuera \(d(i, i') = \sum_j ((f_{ij} - f_{i'j})^2/f_{.j})\) dónde \(f_{.j}\) es la distribución de las columnas en la población, vamos, qué % de rubios, pelirrojos, etc hay en mis datos.
En forma matricial, en notación de Daniel sería 
Esta distancia es equivalente a la euclídea en la matriz Y definida como dividir cada elemento de los perfiles fila por la raíz cuadrada del peso de la columna.
# peso de loas columnas
(f.j <- colSums(tabla_frecuencias))
#> rubio pelirrojo castaño oscuro negro
#> 0.27329076 0.05371901 0.40138993 0.24943651 0.02216379
# peso de las filas
(fi. <- rowSums(tabla_frecuencias))
#> claros azules castaños oscuros
#> 0.2967693 0.1348610 0.3332081 0.2351615Para hacerlo lo hacemos usando matrices
# matriz diagonal con la raíz de los porcentjes totales de las columnas( col masses)
(DC_12 <- diag(1/sqrt(f.j)))
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 1.912879 0.000000 0.000000 0.000000 0.000000
#> [2,] 0.000000 4.314555 0.000000 0.000000 0.000000
#> [3,] 0.000000 0.000000 1.578399 0.000000 0.000000
#> [4,] 0.000000 0.000000 0.000000 2.002258 0.000000
#> [5,] 0.000000 0.000000 0.000000 0.000000 6.717041
# Matriz diagonal con 1/fi.
(DF_1 <- diag(1/fi.))
#> [,1] [,2] [,3] [,4]
#> [1,] 3.36962 0.000000 0.000000 0.000000
#> [2,] 0.00000 7.415042 0.000000 0.000000
#> [3,] 0.00000 0.000000 3.001127 0.000000
#> [4,] 0.00000 0.000000 0.000000 4.252396Matriz Y
# se puede hacer usando los perfiles fila o directamente utilizando DF_1 y DC_12
# Y <- perfiles_fila %*% DC_12
Y <- DF_1 %*% as.matrix(tabla_frecuencias) %*% DC_12
rownames(Y) <- rownames(tabla_frecuencias)
colnames(Y) <- colnames(tabla_frecuencias)
Y
#> rubio pelirrojo castaño oscuro negro
#> claros 0.8329499 0.3167648 0.5834082 0.2382433 0.01700517
#> azules 0.8685217 0.2283469 0.5297968 0.3067526 0.02806563
#> castaños 0.3698521 0.2042969 0.8087737 0.4650114 0.09844593
#> oscuros 0.1497302 0.1654142 0.5080629 0.9883349 0.45602916En esta tabla Y, la distancia euclídea entre filas coincide con la distancia ponderada que habíamos definido dónde la distancia entre dos filas venía ponderada por el peso de cada columna.
Podríamos ahora plantearnos utilizar una descomposición en valores y vectores propios sobre esta tabla, pero tendríamos el problema de que el peso de cada fila sería el mismo, por eso se hace necesario tener en cuenta el peso de cada fila.
Podemos construir ahora una matriz Z dónde se pondere por el peso de las filas y el de las columnas.
# cremaos matriz diagonal con 1/sqrt(fi.)
(DF_12 <- diag(1 / sqrt(fi.)))
#> [,1] [,2] [,3] [,4]
#> [1,] 1.835653 0.000000 0.000000 0.000000
#> [2,] 0.000000 2.723057 0.000000 0.000000
#> [3,] 0.000000 0.000000 1.732376 0.000000
#> [4,] 0.000000 0.000000 0.000000 2.062134Creamos matriz Z como
Z <- DF_12 %*% as.matrix(tabla_frecuencias) %*% DC_12
rownames(Z) <- rownames(tabla_frecuencias)
colnames(Z) <- colnames(tabla_frecuencias)
Z
#> rubio pelirrojo castaño oscuro negro
#> claros 0.45376229 0.17256250 0.3178206 0.1297867 0.009263827
#> azules 0.31895094 0.08385681 0.1945596 0.1126501 0.010306662
#> castaños 0.21349407 0.11792869 0.4668580 0.2684240 0.056827106
#> oscuros 0.07260933 0.08021509 0.2463773 0.4792778 0.221144304Sobre esta matriz Z que no es más que la tabla de frecuencias relativas estandarizada por el peso de las filas y el de las columnas podemos diagonalizar la matriz Z’Z. Esta matriz tiene un valor propio igual a 1, pero los importantes son los siguientes.
res_diag <- eigen(t(Z) %*% Z)
res_diag$values
#> [1] 1.000000e+00 1.873957e-01 2.847581e-02 9.026139e-04 -5.424744e-18
res_diag$vectors
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] -0.5227722 -0.64488569 0.50331668 -0.21984084 0.09578107
#> [2,] -0.2317736 -0.11671207 0.06710395 0.91248080 -0.30908759
#> [3,] -0.6335534 -0.02776729 -0.74923836 -0.04663792 0.18521831
#> [4,] -0.4994362 0.65005451 0.30376531 -0.21371886 -0.43593979
#> [5,] -0.1488751 0.38361288 0.29755318 0.26682945 0.81911020Teniendo la matriz Y, que son los perfiles (porcentajes) fila ponderados por el peso de las columnas, podemos proyectar esas filas sobre las dimensiones obtenidas por los vectores propios obtenidos asociados a los autovalores menores que 1. Esa será la mejor representación de las filas en un subespacio de las columnas.
# proyeccion 1. con valor menor que 1
vector_propio1 <- res_diag$vectors[,2]
vector_propio2 <- res_diag$vectors[,3]
(coord1 <- Y %*% vector_propio1 )
#> [,1]
#> claros -0.42893286
#> azules -0.39128686
#> castaños 0.05523421
#> oscuros 0.68743802
(coord2 <- Y %*% vector_propio2 )
#> [,1]
#> claros 0.08081194
#> azules 0.15705214
#> castaños -0.23555524
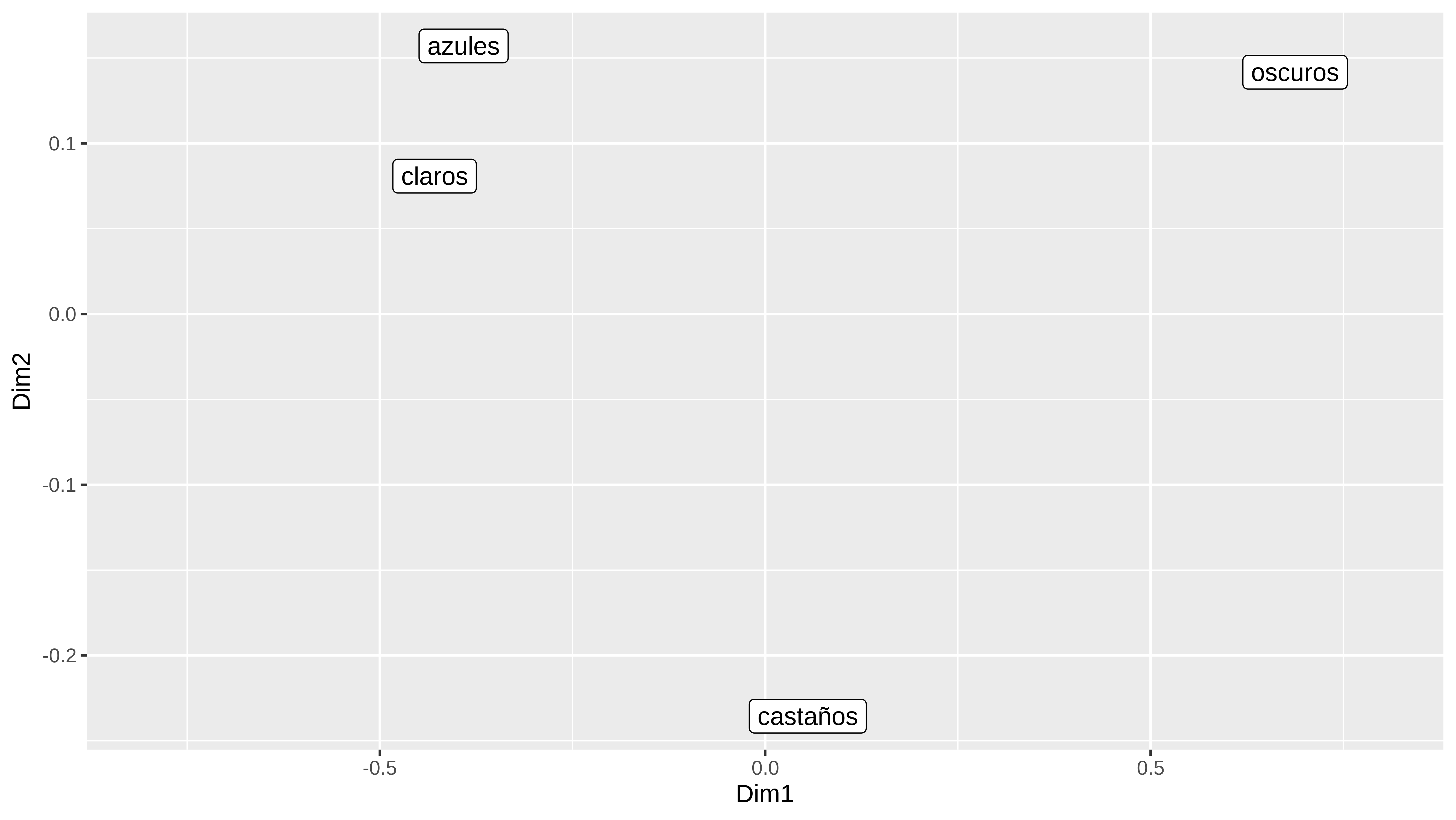
#> oscuros 0.14171621Y ya lo puedo pintar
library(tidyverse)
(to_plot <- data.frame(Dim1 = coord1[,1], Dim2 = coord2[,1], color_ojos= rownames(Y)))
#> Dim1 Dim2 color_ojos
#> claros -0.42893286 0.08081194 claros
#> azules -0.39128686 0.15705214 azules
#> castaños 0.05523421 -0.23555524 castaños
#> oscuros 0.68743802 0.14171621 oscurosProyección de las columnas
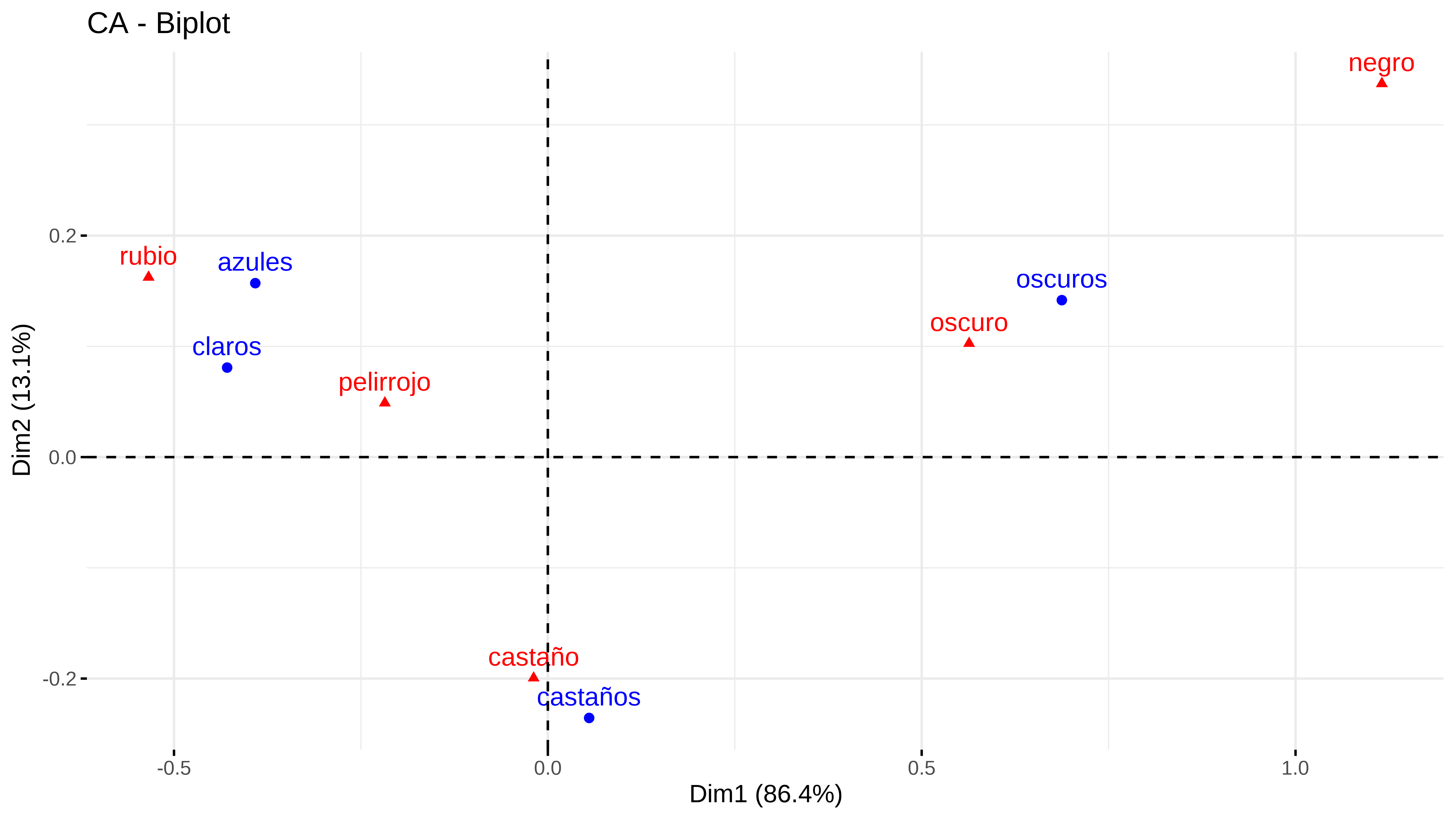
La proyección de las columnas en un subespacio de las filas se hace de manera análoga , solo que en vez de diagonalizar Z’Z se hace con Z Z’, que tiene los mismos valores propios que los obtenidos.
De aquí viene la relación baricéntrica entre las filas y las columnas.
Relación con la distancia Chi-cuadrado
Si se desarrolla la expresión de la distancia Chi-cuadrado , tal como se hace en el libro de Daniel Peña se llega a que se corresponde con la distancia euclídea en la matriz Y que son los perfiles filas ponderados por el peso de cada columna.
Esta implicación es importante, puesto que al descomponer el estadístico Chi-cuadrado que nos mide la asociación entre variables categóricas (filas y columnas), estamos descubriendo qué filas están asociados con determinadas columnas.
Uso con FactoMineR
Sólo trataba de dar una pequeña explicación de la relación entre el análisis de correspondencias y la diagonalización de matrices. Hay mucha más explicación en los libros que he enlazado al principio. En el día a día, podemos usar librerías específicas para calcular este análisis, como FactoMineR en R o prince en python.
Veamos como se usa con FactoMiner
library(FactoMineR)
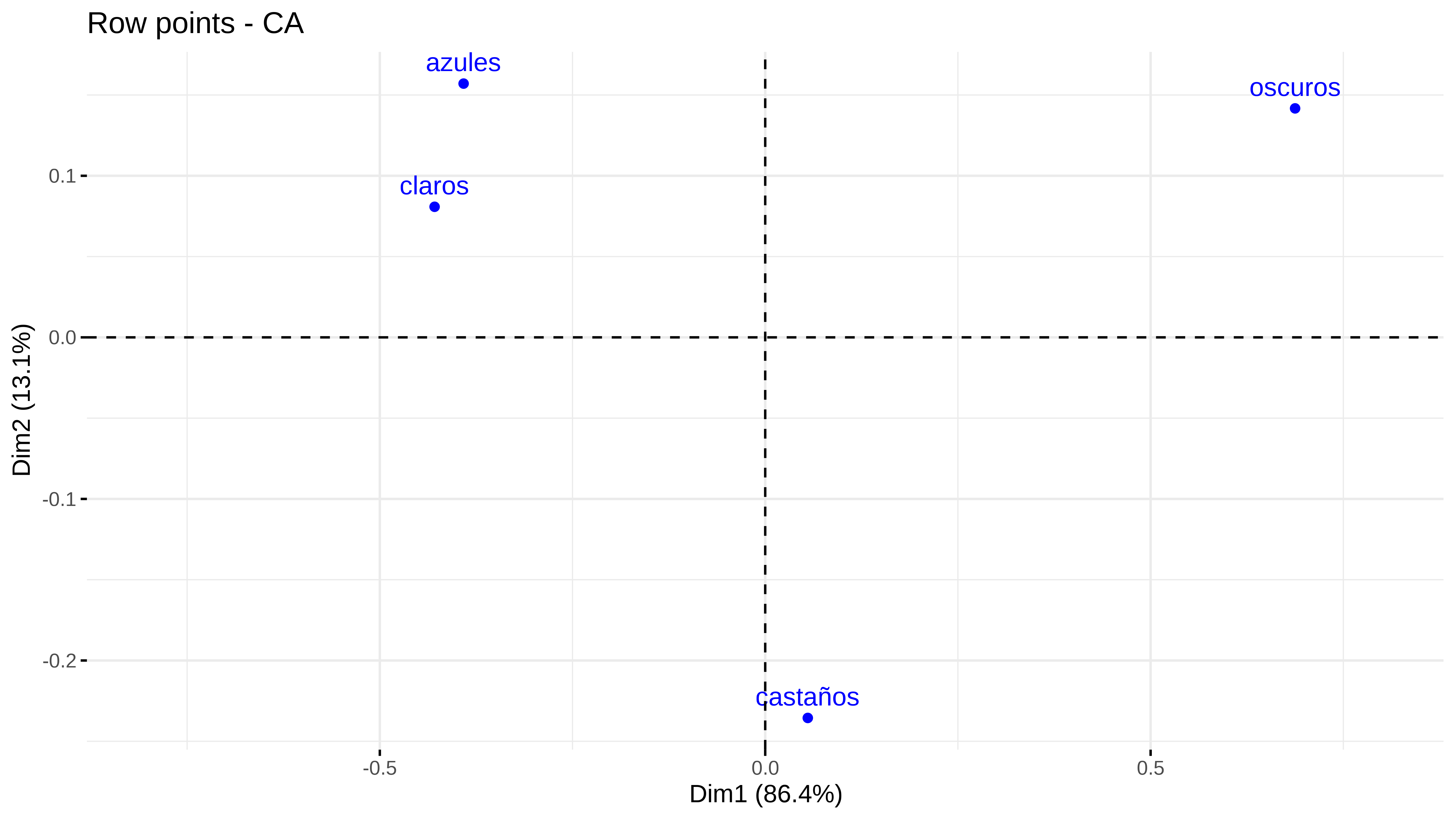
library(factoextra) # pa los dibujitosres_ca <- CA(df_tabla, graph = FALSE)Y podemos pintar las filas en el espacio de las columnas
Y vemos que las coordenadas son las mismas que hemos obtenido nosotros antes
res_ca$row$coord
#> Dim 1 Dim 2 Dim 3
#> claros -0.42893286 0.08081194 0.032336831
#> azules -0.39128686 0.15705214 -0.065353061
#> castaños 0.05523421 -0.23555524 -0.005724586
#> oscuros 0.68743802 0.14171621 0.004781725to_plot
#> Dim1 Dim2 color_ojos
#> claros -0.42893286 0.08081194 claros
#> azules -0.39128686 0.15705214 azules
#> castaños 0.05523421 -0.23555524 castaños
#> oscuros 0.68743802 0.14171621 oscurosLa representación conjunta.
La librería FactoMineR junto con factoextra devuelven también múltiples ayudas a la interpretación como la contribución de cada fila o columna a la estructura factorial etc. Por otro lado, la librería FactoInvestigate que toma como input un análisis factorial (pca, ca o mca), devuelve un informe en inglés (en Rmd) describiendo lo que significa cada dimensión obtenida.