library(tidyverse)
library(dagitty)
library(ggdag)
library(patchwork)
g <- dagitty("dag{
M -> D ;
B2 -> D;
B1 -> M;
U -> M;
U -> D
}")
coords <-
list(
x = c(B1 = 1, M = 2, U = 3.5, D = 5, B2 = 6),
y = c(B1 = 0, M = 0, U = 1, D = 0, B2 = 0)
)
coordinates(g) <- coords
ggdag(g) +
theme_void()Pluralista
Ando viendo los vídeos de Richard McElreath , Statistical Rethinking 2022 y ciertamente me están gustando mucho. En la segunda edición de su libro hace hincapié en temas de inferencia causal. Cuenta bastante bien todo el tema de los “confounders”, “forks”, “colliders” y demás. Además lo hace simulando datos, por lo que entiende todo de forma muy sencilla. Un par de conceptos que me han llamado la atención son por ejemplo cuando dice que condicionar por una variable no significa lo mismo en un modelo de regresión al uso que en uno bayesiano, en el segundo caso significa incluir esa variable en la distribución conjunta. Esto permite por ejemplo que bajo el marco de un modelo bayesiano se pueda condicionar incluso por un “collider” cosa que los entendidos de la inferencia causal prohíben expresamente pues eso abre un camino no causal en el DAG definido.
Según la RAE , pluralismo significa
pluralismo 1. m. Sistema por el cual se acepta o reconoce la pluralidad de doctrinas o posiciones.
y en los videos se toma dicha postura, por ejemplo, se especifica el modelo teórico utilizando los diagramas causales y el Back door criterio para ver sobre qué variables hay que condicionar o no , para ver el efecto total de X sobre Y o para estimar el efecto directo.
Hay un ejemplo muy bueno en este post de Richard.
Nota: Este post es simplemente para entender un poco el post de Richard, el mérito es totalmente de él.
Básicamente es una situación dónde se quiere estimar el efecto que tiene sobre el número de hijos que tiene una mujer, el número de hijos que tuvo su madre. En el diagrama causal también se indica la influencia que tiene el orden de nacimiento de de la madre y de la hija.
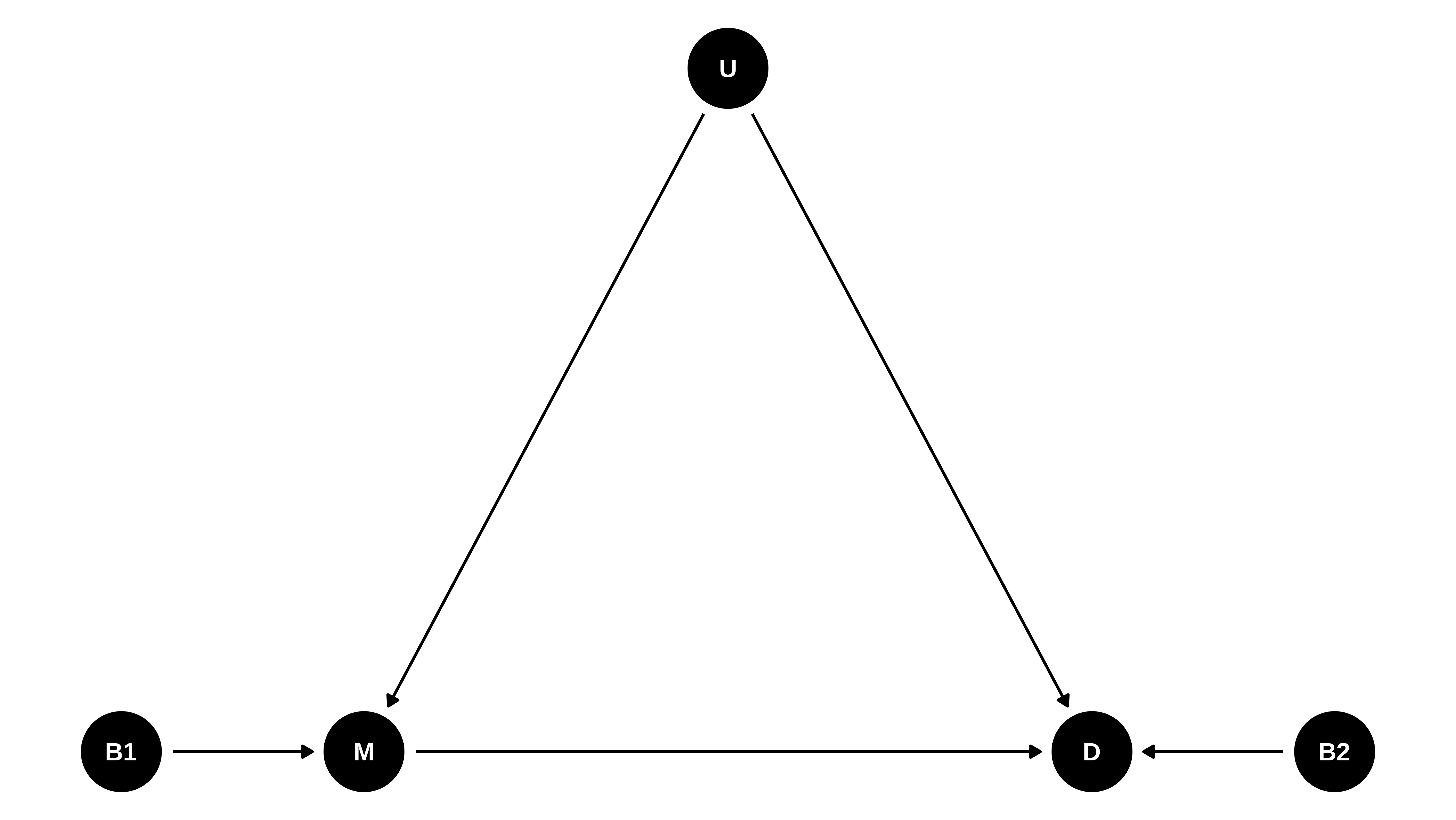
Diagrama causal:
- M: Número de hijos de la madre
- D: Número de hijos de la hija
- B1: Orden de nacimiento de la madre
- B2: Orden de nacimiento de la hija
- U: Variable no medida en los datos, que pudiera ser cosas como influencia del entorno social y económico dónde viven madre e hija, que influye en las decisión del número de hijos de ambas.
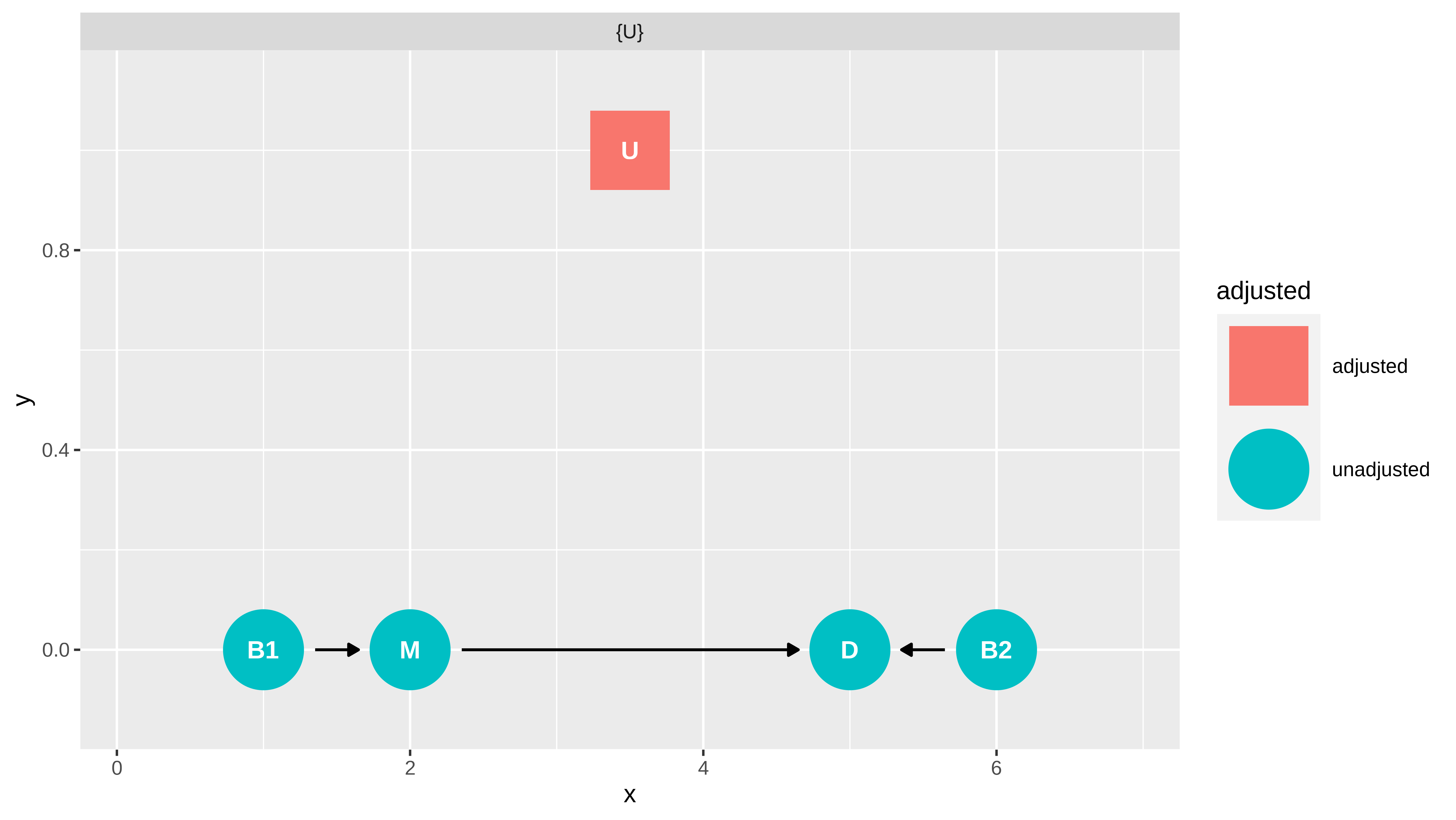
Si queremos estimar el efecto global o el directo de M sobre D, habría que condicionar por U (siguiendo el backdoor criterio), y al ser no observable, no se puede estimar.
adjustmentSets(g, exposure = "M", outcome = "D", effect = "total" )
#> { U }
adjustmentSets(g, exposure = "M", outcome = "D", effect = "direct" )
#> { U }¿Cómo podemos “estimar” el efecto de M sobre D dado que no podemos condicionar (en el sentido clásico) sobre U? .
Richard propone lo que el llama “full luxury bayesian” que consiste en estimar a la vez todo el DAG y luego generar simulaciones usando la distribución conjunta obtenida para medir el efecto de la “intervención” y poder obtener el efecto causal.
Nótese que cuando en el DAG las relaciones se pueden expresar como modelos lineales, se puede estimar todo el DAG usando técnicas como los modelos de ecuaciones estructurales o el path analysis.
Simulación
Simulamos unos datos de forma qué vamos a conocer la “verdad” de la relaciones entre variables, que para eso simulamos.
set.seed(1908)
N <- 1000 # número de pares, 1000 madres y 1000 hijas
U <- rnorm(N,0,1) # Simulamos el confounder
# orden de nacimiento y
B1 <- rbinom(N,size=1,prob=0.5) # 50% de madres nacieeron en primer lugar
M <- rnorm( N , 2 * B1 + U )
B2 <- rbinom(N,size=1,prob=0.5) # 50% son las primogénitas
D <- rnorm( N , 2 *B2 + U + 0 * M )En esta simulación se ha forzado que el efecto del número de hijos de la madre sobre el núemro de hijos de la hija sea nulo. Por tanto sabemos que el efecto de M sobre D es 0..
Si hacemos un modelo sin condicionar, tenemos sesgo
lm(D ~ M)
#>
#> Call:
#> lm(formula = D ~ M)
#>
#> Coefficients:
#> (Intercept) M
#> 0.7108 0.2930Condicionando por B1 también, de hecho tenemos la situación de amplificación del sesgo
lm(D ~ M + B1)
#>
#> Call:
#> lm(formula = D ~ M + B1)
#>
#> Coefficients:
#> (Intercept) M B1
#> 1.0356 0.4606 -1.0441lm(D ~ M + B1 +B2 )
#>
#> Call:
#> lm(formula = D ~ M + B1 + B2)
#>
#> Coefficients:
#> (Intercept) M B1 B2
#> -0.01621 0.46913 -0.91307 2.01487lm(D ~ M + B2)
#>
#> Call:
#> lm(formula = D ~ M + B2)
#>
#> Coefficients:
#> (Intercept) M B2
#> -0.3204 0.3231 2.0550En esta situación, no podemos estimar el efecto de M sobre D utilizando un solo modelo.
Una forma de estimar el efecto de M sobre D es tirar de path analysis, que en este caso se puede al ser las relaciones lineales.
Sea:
- b: Efecto de B1 sobre M
- m: Efecto de M sobre D
Se tiene que
\[Cov(B1, D ) = b\cdot m \cdot Var(B1)\] Y como
\[b = \dfrac{Cov(B1,M)}{Var(B1)} \]
Podemos estimar \(m\) como
\[m = \dfrac{Cov(B1,D)}{b \cdot Var(B1)} = \dfrac{Cov(B1,D)}{Cov(B1,M)} \] Y
(m_hat = cov(B1,D) / cov(B1,M))
#> [1] -0.0563039y esta estimación está menos sesgada, antes era del orden de 0.1 o 0.2 y ahora la estimación es del orden 0.01. Pero con esta estimación no tenemos información de su distribución sino sólo de esta estimación puntual. Y si las relaciones no fueran lineales no podría usarse, en cambio la siguiente aproximación si funciona
Full luxury bayes
Utilizamos la librería de Richard rethinking y también cmdstanr para expresar el modelo causal completo y ajustarlo con Stan.
Ahora estimamos el DAG completo, aquí es dónde es diferente de la aproximación causal de Pearl, de esta forma podemos “condicionar” incluso por los colliders, porque condicionar en este marco significa meter esa información dentro de la distribución conjunta.
library(cmdstanr)
library(rethinking)
set_cmdstan_path("~/Descargas/cmdstan/")
# No metemos U al ser no observable
dat <- list(
N = N,
M = M,
D = D,
B1 = B1,
B2 = B2
)
set.seed(1908)
flbi <- ulam(
alist(
# mom model
M ~ normal( mu , sigma ),
mu <- a1 + b*B1 + k*U[i],
# daughter model
D ~ normal( nu , tau ),
nu <- a2 + b*B2 + m*M + k*U[i],
# B1 and B2
B1 ~ bernoulli(p),
B2 ~ bernoulli(p),
# unmeasured confound
vector[N]:U ~ normal(0,1),
# priors
c(a1,a2,b,m) ~ normal( 0 , 0.5 ),
c(k,sigma,tau) ~ exponential( 1 ),
p ~ beta(2,2)
), data=dat , chains=4 , cores=4 , warmup = 500, iter=2500 , cmdstan=TRUE )
#> Running MCMC with 4 parallel chains, with 1 thread(s) per chain...
#>
#> Chain 1 Iteration: 1 / 2500 [ 0%] (Warmup)
#> Chain 2 Iteration: 1 / 2500 [ 0%] (Warmup)
#> Chain 3 Iteration: 1 / 2500 [ 0%] (Warmup)
#> Chain 4 Iteration: 1 / 2500 [ 0%] (Warmup)
#> Chain 4 Iteration: 100 / 2500 [ 4%] (Warmup)
#> Chain 3 Iteration: 100 / 2500 [ 4%] (Warmup)
#> Chain 4 Iteration: 200 / 2500 [ 8%] (Warmup)
#> Chain 1 Iteration: 100 / 2500 [ 4%] (Warmup)
#> Chain 2 Iteration: 100 / 2500 [ 4%] (Warmup)
#> Chain 3 Iteration: 200 / 2500 [ 8%] (Warmup)
#> Chain 1 Iteration: 200 / 2500 [ 8%] (Warmup)
#> Chain 4 Iteration: 300 / 2500 [ 12%] (Warmup)
#> Chain 2 Iteration: 200 / 2500 [ 8%] (Warmup)
#> Chain 4 Iteration: 400 / 2500 [ 16%] (Warmup)
#> Chain 1 Iteration: 300 / 2500 [ 12%] (Warmup)
#> Chain 3 Iteration: 300 / 2500 [ 12%] (Warmup)
#> Chain 1 Iteration: 400 / 2500 [ 16%] (Warmup)
#> Chain 2 Iteration: 300 / 2500 [ 12%] (Warmup)
#> Chain 3 Iteration: 400 / 2500 [ 16%] (Warmup)
#> Chain 4 Iteration: 500 / 2500 [ 20%] (Warmup)
#> Chain 4 Iteration: 501 / 2500 [ 20%] (Sampling)
#> Chain 2 Iteration: 400 / 2500 [ 16%] (Warmup)
#> Chain 3 Iteration: 500 / 2500 [ 20%] (Warmup)
#> Chain 3 Iteration: 501 / 2500 [ 20%] (Sampling)
#> Chain 1 Iteration: 500 / 2500 [ 20%] (Warmup)
#> Chain 1 Iteration: 501 / 2500 [ 20%] (Sampling)
#> Chain 4 Iteration: 600 / 2500 [ 24%] (Sampling)
#> Chain 2 Iteration: 500 / 2500 [ 20%] (Warmup)
#> Chain 2 Iteration: 501 / 2500 [ 20%] (Sampling)
#> Chain 3 Iteration: 600 / 2500 [ 24%] (Sampling)
#> Chain 1 Iteration: 600 / 2500 [ 24%] (Sampling)
#> Chain 4 Iteration: 700 / 2500 [ 28%] (Sampling)
#> Chain 2 Iteration: 600 / 2500 [ 24%] (Sampling)
#> Chain 3 Iteration: 700 / 2500 [ 28%] (Sampling)
#> Chain 1 Iteration: 700 / 2500 [ 28%] (Sampling)
#> Chain 4 Iteration: 800 / 2500 [ 32%] (Sampling)
#> Chain 2 Iteration: 700 / 2500 [ 28%] (Sampling)
#> Chain 3 Iteration: 800 / 2500 [ 32%] (Sampling)
#> Chain 1 Iteration: 800 / 2500 [ 32%] (Sampling)
#> Chain 4 Iteration: 900 / 2500 [ 36%] (Sampling)
#> Chain 2 Iteration: 800 / 2500 [ 32%] (Sampling)
#> Chain 3 Iteration: 900 / 2500 [ 36%] (Sampling)
#> Chain 1 Iteration: 900 / 2500 [ 36%] (Sampling)
#> Chain 4 Iteration: 1000 / 2500 [ 40%] (Sampling)
#> Chain 2 Iteration: 900 / 2500 [ 36%] (Sampling)
#> Chain 3 Iteration: 1000 / 2500 [ 40%] (Sampling)
#> Chain 1 Iteration: 1000 / 2500 [ 40%] (Sampling)
#> Chain 4 Iteration: 1100 / 2500 [ 44%] (Sampling)
#> Chain 2 Iteration: 1000 / 2500 [ 40%] (Sampling)
#> Chain 3 Iteration: 1100 / 2500 [ 44%] (Sampling)
#> Chain 1 Iteration: 1100 / 2500 [ 44%] (Sampling)
#> Chain 4 Iteration: 1200 / 2500 [ 48%] (Sampling)
#> Chain 2 Iteration: 1100 / 2500 [ 44%] (Sampling)
#> Chain 3 Iteration: 1200 / 2500 [ 48%] (Sampling)
#> Chain 1 Iteration: 1200 / 2500 [ 48%] (Sampling)
#> Chain 4 Iteration: 1300 / 2500 [ 52%] (Sampling)
#> Chain 2 Iteration: 1200 / 2500 [ 48%] (Sampling)
#> Chain 3 Iteration: 1300 / 2500 [ 52%] (Sampling)
#> Chain 1 Iteration: 1300 / 2500 [ 52%] (Sampling)
#> Chain 4 Iteration: 1400 / 2500 [ 56%] (Sampling)
#> Chain 2 Iteration: 1300 / 2500 [ 52%] (Sampling)
#> Chain 3 Iteration: 1400 / 2500 [ 56%] (Sampling)
#> Chain 1 Iteration: 1400 / 2500 [ 56%] (Sampling)
#> Chain 4 Iteration: 1500 / 2500 [ 60%] (Sampling)
#> Chain 2 Iteration: 1400 / 2500 [ 56%] (Sampling)
#> Chain 3 Iteration: 1500 / 2500 [ 60%] (Sampling)
#> Chain 4 Iteration: 1600 / 2500 [ 64%] (Sampling)
#> Chain 1 Iteration: 1500 / 2500 [ 60%] (Sampling)
#> Chain 2 Iteration: 1500 / 2500 [ 60%] (Sampling)
#> Chain 3 Iteration: 1600 / 2500 [ 64%] (Sampling)
#> Chain 4 Iteration: 1700 / 2500 [ 68%] (Sampling)
#> Chain 1 Iteration: 1600 / 2500 [ 64%] (Sampling)
#> Chain 2 Iteration: 1600 / 2500 [ 64%] (Sampling)
#> Chain 3 Iteration: 1700 / 2500 [ 68%] (Sampling)
#> Chain 4 Iteration: 1800 / 2500 [ 72%] (Sampling)
#> Chain 1 Iteration: 1700 / 2500 [ 68%] (Sampling)
#> Chain 2 Iteration: 1700 / 2500 [ 68%] (Sampling)
#> Chain 3 Iteration: 1800 / 2500 [ 72%] (Sampling)
#> Chain 4 Iteration: 1900 / 2500 [ 76%] (Sampling)
#> Chain 1 Iteration: 1800 / 2500 [ 72%] (Sampling)
#> Chain 2 Iteration: 1800 / 2500 [ 72%] (Sampling)
#> Chain 3 Iteration: 1900 / 2500 [ 76%] (Sampling)
#> Chain 4 Iteration: 2000 / 2500 [ 80%] (Sampling)
#> Chain 1 Iteration: 1900 / 2500 [ 76%] (Sampling)
#> Chain 2 Iteration: 1900 / 2500 [ 76%] (Sampling)
#> Chain 3 Iteration: 2000 / 2500 [ 80%] (Sampling)
#> Chain 4 Iteration: 2100 / 2500 [ 84%] (Sampling)
#> Chain 1 Iteration: 2000 / 2500 [ 80%] (Sampling)
#> Chain 2 Iteration: 2000 / 2500 [ 80%] (Sampling)
#> Chain 3 Iteration: 2100 / 2500 [ 84%] (Sampling)
#> Chain 4 Iteration: 2200 / 2500 [ 88%] (Sampling)
#> Chain 1 Iteration: 2100 / 2500 [ 84%] (Sampling)
#> Chain 2 Iteration: 2100 / 2500 [ 84%] (Sampling)
#> Chain 3 Iteration: 2200 / 2500 [ 88%] (Sampling)
#> Chain 4 Iteration: 2300 / 2500 [ 92%] (Sampling)
#> Chain 1 Iteration: 2200 / 2500 [ 88%] (Sampling)
#> Chain 2 Iteration: 2200 / 2500 [ 88%] (Sampling)
#> Chain 3 Iteration: 2300 / 2500 [ 92%] (Sampling)
#> Chain 4 Iteration: 2400 / 2500 [ 96%] (Sampling)
#> Chain 1 Iteration: 2300 / 2500 [ 92%] (Sampling)
#> Chain 2 Iteration: 2300 / 2500 [ 92%] (Sampling)
#> Chain 3 Iteration: 2400 / 2500 [ 96%] (Sampling)
#> Chain 1 Iteration: 2400 / 2500 [ 96%] (Sampling)
#> Chain 4 Iteration: 2500 / 2500 [100%] (Sampling)
#> Chain 4 finished in 17.1 seconds.
#> Chain 2 Iteration: 2400 / 2500 [ 96%] (Sampling)
#> Chain 3 Iteration: 2500 / 2500 [100%] (Sampling)
#> Chain 3 finished in 17.5 seconds.
#> Chain 1 Iteration: 2500 / 2500 [100%] (Sampling)
#> Chain 1 finished in 17.6 seconds.
#> Chain 2 Iteration: 2500 / 2500 [100%] (Sampling)
#> Chain 2 finished in 17.9 seconds.
#>
#> All 4 chains finished successfully.
#> Mean chain execution time: 17.6 seconds.
#> Total execution time: 18.0 seconds.post <- extract.samples(flbi)
precis(flbi)
#> mean sd 5.5% 94.5% n_eff Rhat4
#> m 0.01029393 0.04047150 -0.05430275 0.07409054 890.4789 1.0018319
#> b 1.98864256 0.05811342 1.89487725 2.08168275 3042.1496 1.0007825
#> a2 0.02836364 0.07310509 -0.08729441 0.14659932 1335.7564 1.0027553
#> a1 0.06834714 0.05394291 -0.01785119 0.15621615 3747.6036 1.0007151
#> tau 0.98041340 0.03617180 0.92352906 1.03914055 2745.6394 1.0007016
#> sigma 1.07286195 0.05249312 0.98902178 1.15557275 909.1510 1.0015771
#> k 0.98545837 0.05638324 0.89516212 1.07461055 828.2759 1.0013545
#> p 0.48012384 0.01111044 0.46233213 0.49808700 16117.4910 0.9996995Vemos que no aparece la estimación de U, pero en la posterior se ha estimado un valor de U para cada uno de las observaciones. 1000 observaciones y
dim(post$U)
#> [1] 8000 1000
post$U[1:4, 1:5]
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] 0.382053 -0.4087260 -1.5231200 0.486262 0.00381229
#> [2,] 0.733459 0.2971870 0.0441252 -1.424160 -0.98469300
#> [3,] 0.254011 -0.0201819 -0.7499000 -1.444340 -0.51772400
#> [4,] 0.468004 0.1923180 -1.8694400 -1.314570 -0.43902700Efecto de M sobre D.
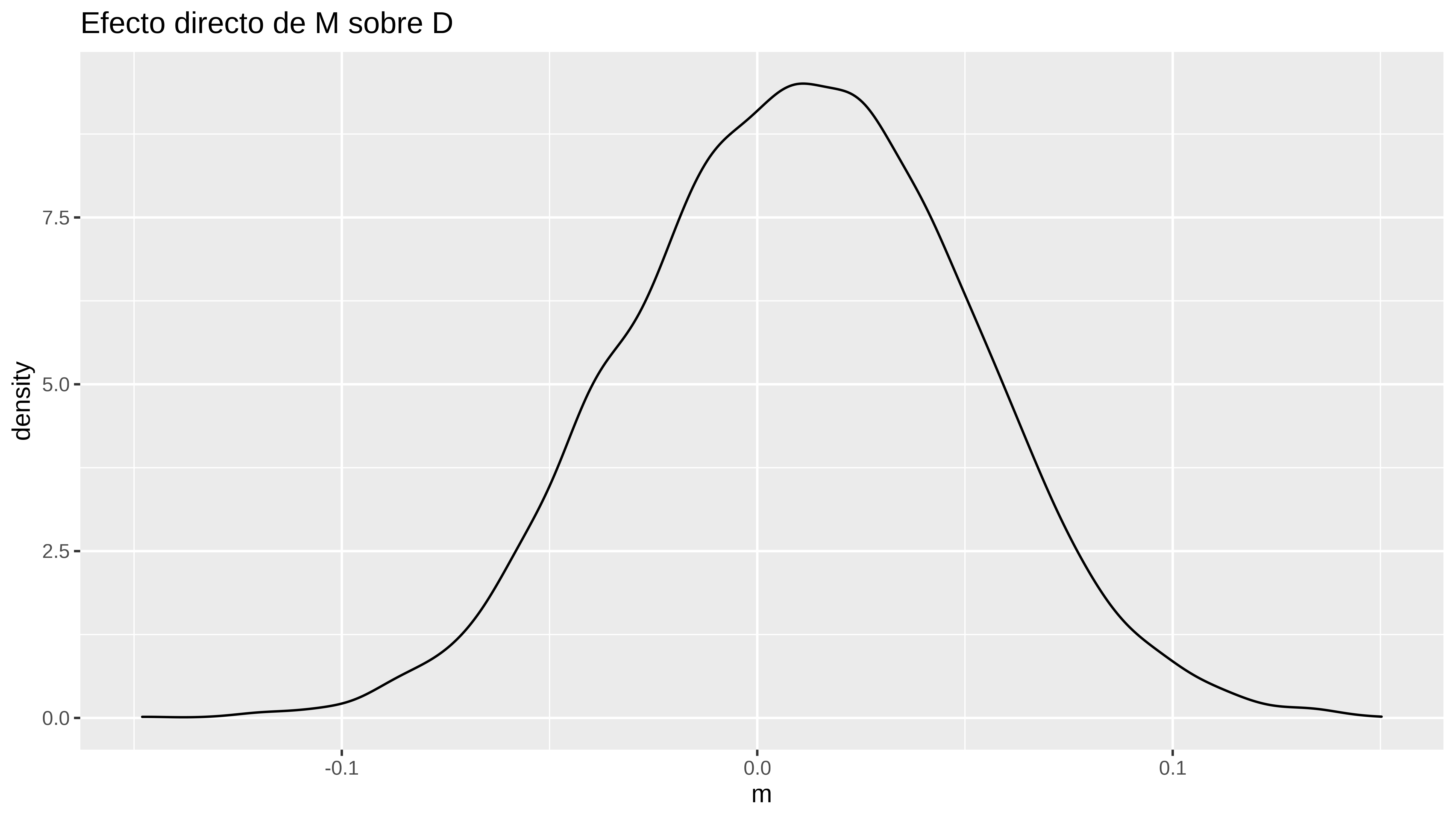
Este era el efecto que queríamos obtener y el cuál no podíamos estimar al no poder condicionar sobre U. Aquí es tan sencillo como ver su distribución a posteriori.
quantile(post$m)
#> 0% 25% 50% 75% 100%
#> -0.14804300 -0.01706778 0.01080760 0.03813360 0.15027000
ggplot() +
geom_density(aes(post$m)) +
labs(title = "Efecto directo de M sobre D",
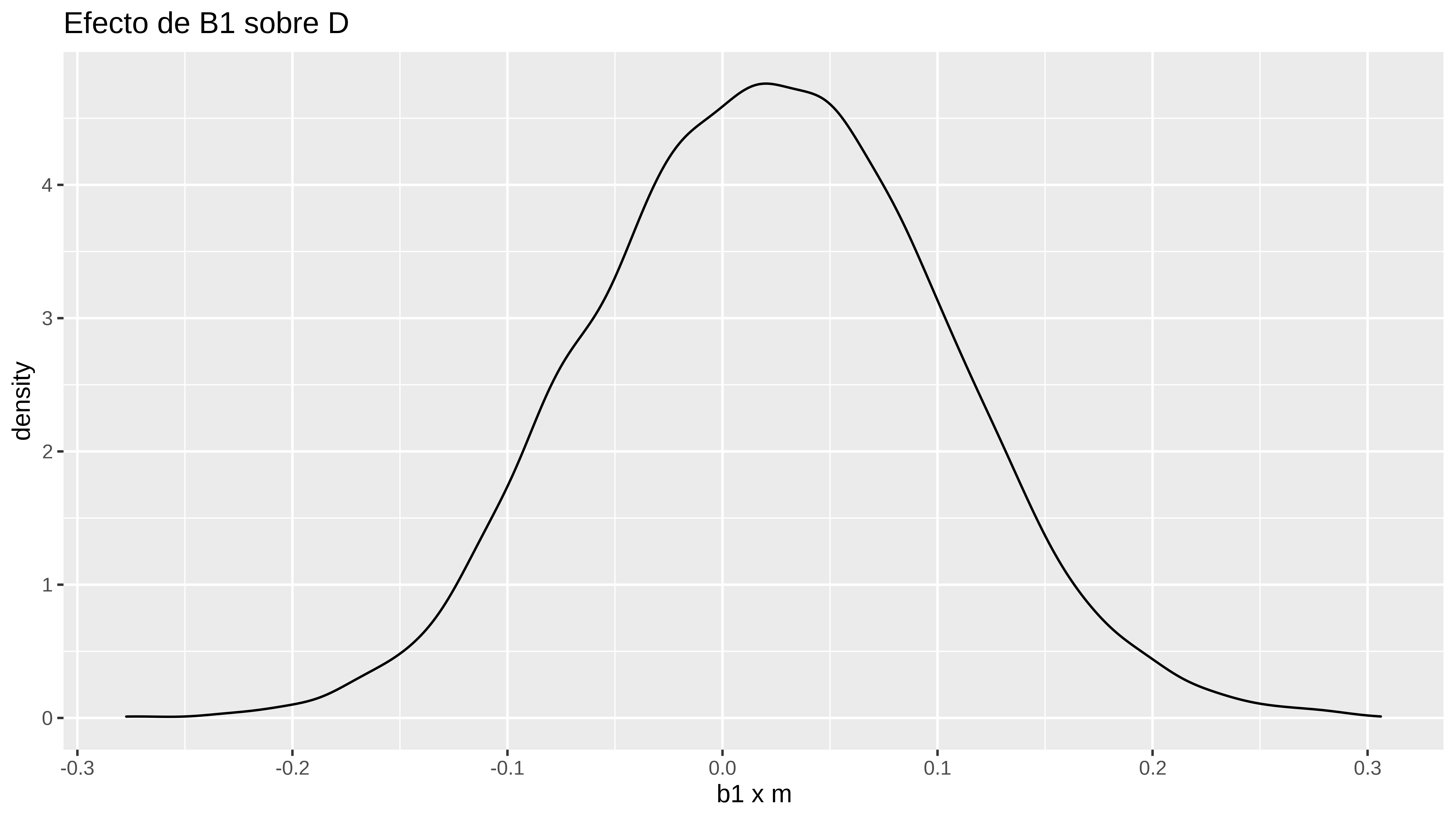
x = "m")Efecto de B1 sobre D
Como ya sabíamos, al haber simulado los datos de forma que las relaciones entre las variables sean lineales, el efecto de B1 sobre D no es más que el efecto de B1 sobre M multiplicado por el efecto de M sobre D.
Utilizando la distribución a posteriori.
Efecto de B1 sobre D, simulando
Tal y como dice en su curso, el efecto causal puede ser visto como hacer una intervención supuesto cierto el modelo causal.
Simplemente utilizamos las posterioris obtenidas y vamos simulando , en primer lugar B1 = 0 y simulamos qué M se obtendría, y lo hacemos también para B1 = 1 y restamos para obtener el efecto causal, que coindice con b * m
#
# B1 = 0
# B1 -> M
M_B1_0 <- with( post , a1 + b*0 + k*0 )
# M -> D
D_B1_0 <- with( post , a2 + b*0 + m*M_B1_0 + k*0 )
# now same but with B1 = 1
M_B1_1 <- with( post , a1 + b*1 + k*0 )
D_B1_1 <- with( post , a2 + b*0 + m*M_B1_1 + k*0 )
# difference to get causal effect
d_D_B1 <- D_B1_1 - D_B1_0
quantile(d_D_B1)
#> 0% 25% 50% 75% 100%
#> -0.27728158 -0.03379382 0.02148739 0.07658919 0.30614657Pues como dice el título , ser pluralista no está tan mal, puedes usar el DAG y el backdoor criterio para entender qué variables ha de tener en cuenta para estimar tu efecto causal, y a partir de ahí podrías usar el “full luxury bayesian” en situaciones más complicadas.