Palabras para Julia ( Parte 3/n)
Tengo una relación extraña con Julia, por un lado me gusta bastante y por otro me parece que aún le falta algo para que lo adopte de forma más seria. Quizá tenga que ver con mi forma de aprender (que seguro que no es óptima), en vez de irme a los tutoriales típicos, me voy directamente a ver cómo se hace algo que me interesa. En este caso hacer modelos bayesianos con Julia usando Turing.
Turing es una librería escrita en Julia para programación probabilística, podría considerarse como un competidor de Stan, aunque todavía es una librería joven. Turing añade sólo una pequeña capa de programación probabilística, y promete cosas como modelos de redes neuronales dónde los pesos sigan una distribución probabilística
No me voy a meter en esos lares, yo soy más prosaico y por el momento sólo quiero ejemplificar con Turing el modelo que cuento en pluralista.
Recordemos que habías simulado unos datos tal que así.
set.seed(1908)
N <- 1000 # número de pares, 1000 madres y 1000 hijas
U <- rnorm(N,0,1) # Simulamos el confounder
# orden de nacimiento y
B1 <- rbinom(N,size=1,prob=0.5) # 50% de madres nacieeron en primer lugar
M <- rnorm( N , 2 * B1 + U )
B2 <- rbinom(N,size=1,prob=0.5) # 50% son las primogénitas
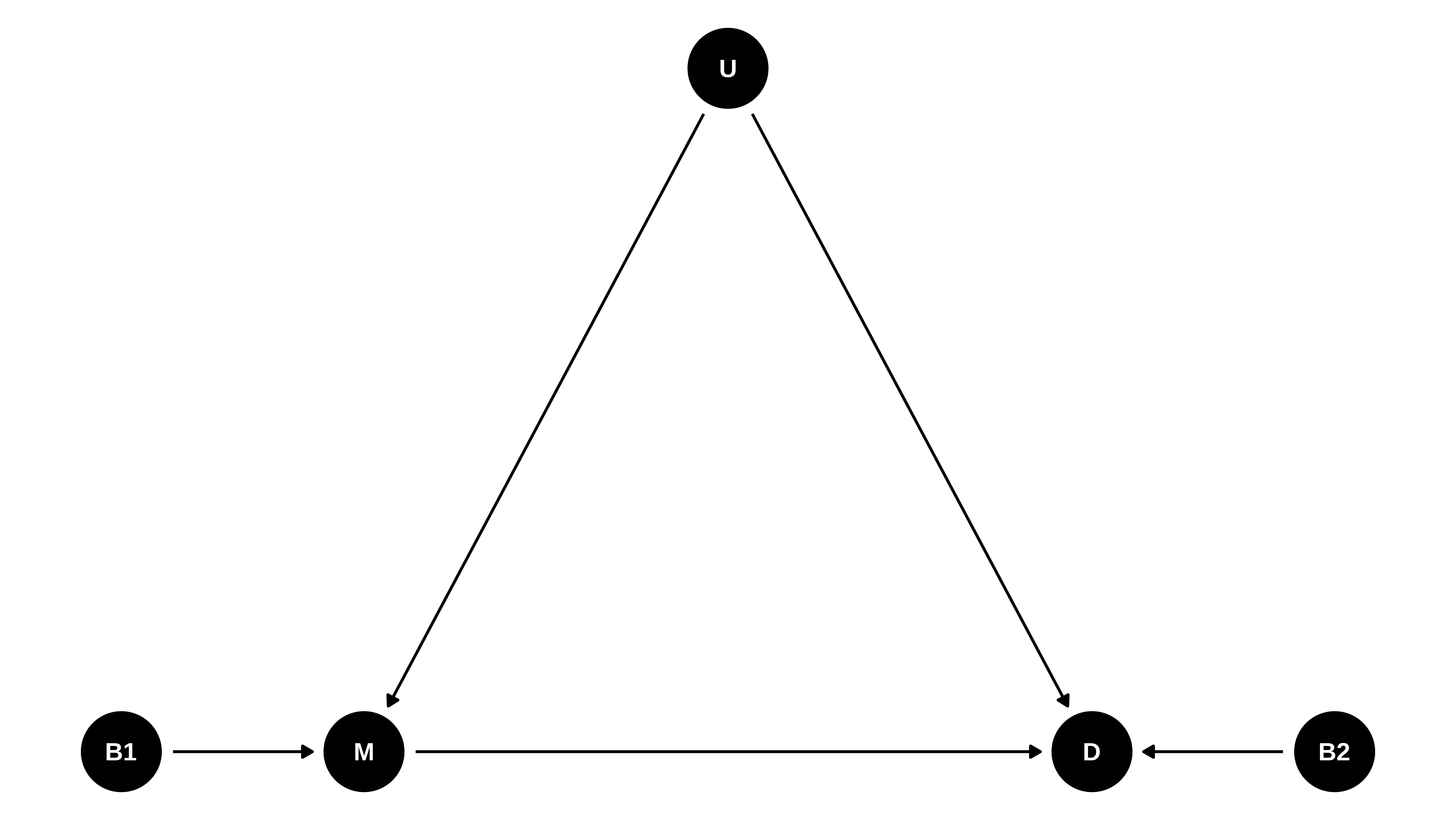
D <- rnorm( N , 2 *B2 + U + 0 * M )En la simulación se ha forzado que el efecto del número de hijos de la madre (M) sobre el número de hijos de la hija (D) sea cero.
El DAG era algo así. En este dag para estimar el efecto de M sobre D, hace falta condicionar por U, pero al ser una variable de confusión no observada, no habría forma de estimarlo de la forma tradicional (a lo Pearl). La solución es estimar el DAG completo.
Ajuste en Turing
Recordemos que nuestra U es una variable que no tenemos, se podría asimilar a una variable con todos sus valores perdidos y cada uno de esos valores perdidos es un parámetro a estimar.
Librerías : Aparte de Turing, hace falta ReverseDiff (diferenciación automática) y alguna más.
using LinearAlgebra, Plots
using Turing
using ReverseDiff, Memoization
using DataFrames
using CSV
using Random
using StatsPlots
using DistributionsLeo los datos simulados que había guardado en un csv previamente
pl = DataFrame(CSV.File("data/pluralista.csv"))
describe(pl)julia> describe(pl)
4×7 DataFrame
Row │ variable mean min median max nmissing eltype
│ Symbol Float64 Real Float64 Real Int64 DataType
─────┼────────────────────────────────────────────────────────────────────
1 │ D 1.00621 -3.55365 0.986136 6.03293 0 Float64
2 │ M 1.00836 -3.91626 0.90395 6.69591 0 Float64
3 │ B1 0.473 0 0.0 1 0 Int64
4 │ B2 0.487 0 0.0 1 0 Int64Nos construimos el modelo con Turing.
Algunas cosas a comentar.
El uso de filldist para crear el vector de U y que cada valor siga una Normal(0,1).
.+para sumar un escalar como a1 con un vector. El uso del “.operacion” es habitual en julia para hacer broadcast.MvNormal al final. Esto lo he leído por ahí para que haga mejor el sampleo.
Al igual que en Stan se tiene que escribir en cierto orden (y si no no funciona bien) porque Turing no es declarativo.
@model function pluralista(D, M, B1, B2)
N = Int(length(D))
# Variable no observada
U ~ filldist(Normal(0, 1), N)
# Prior coeficientes
a1 ~ Normal(0, 0.5)
a2 ~ Normal(0, 0.5)
m ~ Normal(0, 0.5)
b ~ Normal(0, 0.5)
p ~ Beta(2,2)
k ~ Exponential(1)
σ₁ ~ Exponential(1)
σ₂ ~ Exponential(1)
B1 ~ Bernoulli(p)
B2 ~ Bernoulli(p)
# transformed parameters
mu1 = a1 .+ b * B1 + k * U
mu2 = a2 .+ b * B2 + m * M + k * U
# likelihood
M ~ MvNormal(mu1, σ₁ * I)
D ~ MvNormal(mu2, σ₂ * I)
endComparando con el código del mismo modelo en Stan (al final del post) se observa que la sintaxis es parecida.
Muestreo de la posterior en Turing
Hay que usar reversediff porque si no no acaba nunca.
Random.seed!(155)
Turing.setadbackend(:reversediff)
Turing.setrdcache(true)
flbi = sample(
pluralista(pl.D, pl.M, pl.B1, pl.B2),
NUTS(1000, 0.65),
MCMCThreads(),
2_000, 4)julia> flbi = sample(
pluralista(pl.D, pl.M, pl.B1, pl.B2),
NUTS(1000, 0.65),
MCMCThreads(),
2_000, 4)
┌ Info: Found initial step size
└ ϵ = 0.0125
┌ Info: Found initial step size
└ ϵ = 0.025
┌ Info: Found initial step size
└ ϵ = 0.05
┌ Info: Found initial step size
└ ϵ = 0.00625
Chains MCMC chain (2000×1020×4 Array{Float64, 3}):
Iterations = 1001:1:3000
Number of chains = 4
Samples per chain = 2000
Wall duration = 136.29 seconds
Compute duration = 510.14 secondsY ha tardado unos 2 minutos por cadena. Ciertamente no está mal, pero no se acerca a la velocidad de Stan, que lo hace en unos 18 segundos.
Y podemos extraer un resumen de los parámetros que nos interesan con
julia> summarize(flbi[[:a1, :a2, :b, :m, :σ₁, :σ₂]])
Summary Statistics
parameters mean std naive_se mcse ess rhat ess_per_sec
Symbol Float64 Float64 Float64 Float64 Float64 Float64 Float64
a1 0.0682 0.0538 0.0006 0.0009 3268.9064 1.0007 6.4079
a2 0.0326 0.0759 0.0008 0.0024 1015.7923 1.0059 1.9912
m 0.0063 0.0430 0.0005 0.0018 554.1348 1.0096 1.0862
b 1.9865 0.0593 0.0007 0.0012 2403.5462 1.0008 4.7116
σ₁ 1.1427 0.1205 0.0013 0.0049 535.2307 1.0086 1.0492
σ₂ 0.9621 0.0719 0.0008 0.0016 2496.8176 1.0009 4.8944
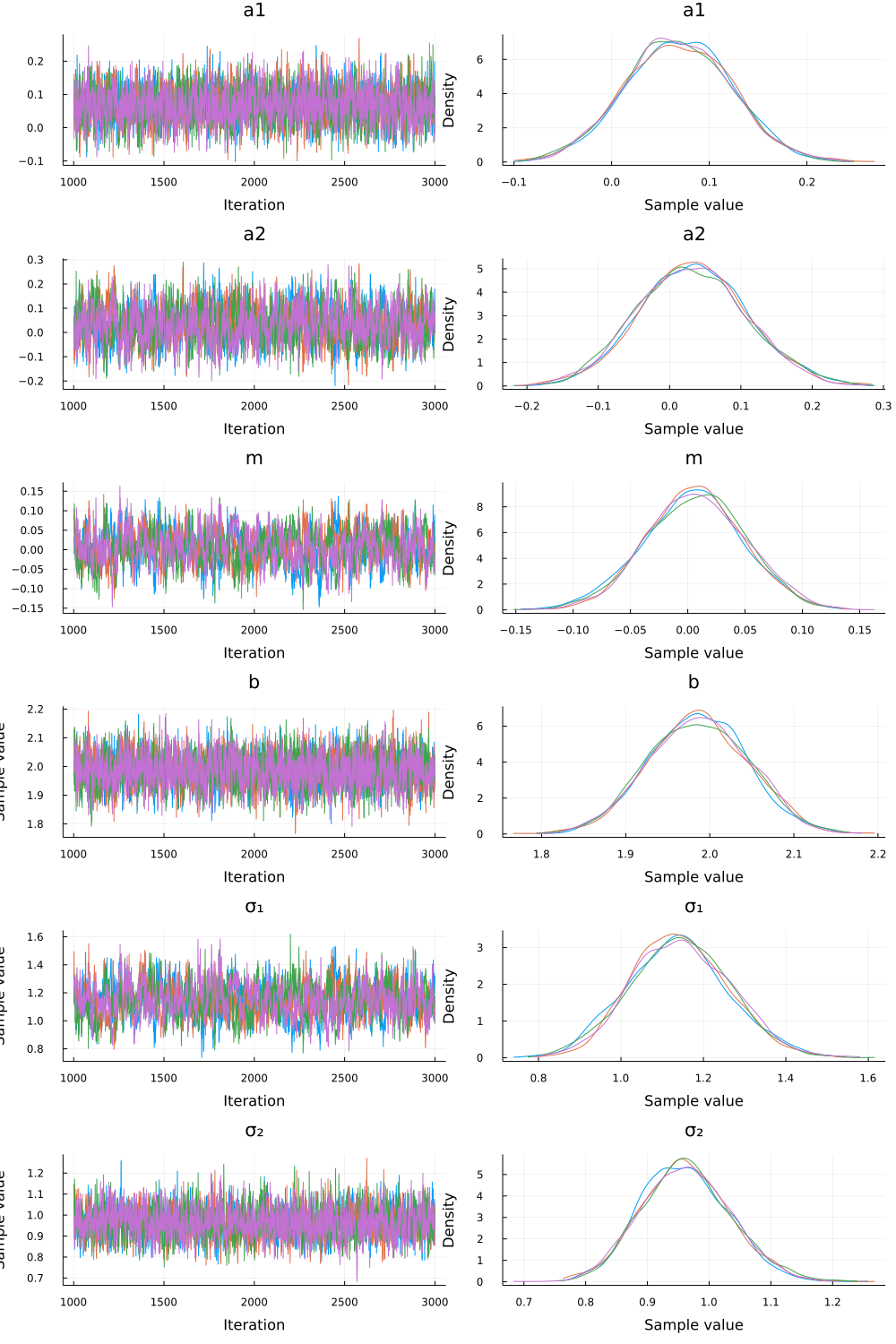
Y efectivamente, lo ha hecho bien y ha recuperado los verdaderos valores de los parámetros y estimado que el efecto de M sobre D es 0.
myplot = plot(flbi[[:a1, :a2, :b, :m, :σ₁, :σ₂]])
savefig(myplot,"plurarlista_turing.png")Reflexiones.
- Me ha parecido fácil escribir un modelo bayesiano como este en Turing
- No he conseguido ver como hacer que me funcione un predict sobre nuevos datos que tengan B1 y B2, pero no M y D. Cuestión de empezar más poco a poco con los tutoriales que hay por ahí.
- Por el momento parece que Stan sigue siendo el estado del arte en estas cosas, aunque lo de integrar Turing con Flux por ejemplo, promete.
Mismo modelo en Stan.
data{
int N;
vector[N] D;
vector[N] M;
int B1[N];
int B2[N];
}
parameters{
vector[N] U;
real m;
real b;
real a2;
real a1;
real<lower=0> tau;
real<lower=0> sigma;
real<lower=0> k;
real<lower=0,upper=1> p;
}
transformed parameters {
vector[N] nu;
vector[N] mu;
for ( i in 1:N ) {
nu[i] = a2 + b * B2[i] + m * M[i] + k * U[i];
}
for ( i in 1:N ) {
mu[i] = a1 + b * B1[i] + k * U[i];
}
}
model{
U ~ normal( 0 , 1 );
a1 ~ normal( 0 , 0.5 );
a2 ~ normal( 0 , 0.5 );
m ~ normal( 0 , 0.5 );
b ~ normal( 0 , 0.5 );
p ~ beta( 2 , 2 );
k ~ exponential( 1 );
sigma ~ exponential( 1 );
tau ~ exponential( 1 );
B2 ~ bernoulli( p );
B1 ~ bernoulli( p );
D ~ normal( nu , tau );
M ~ normal( mu , sigma );
}
// genero point_loglikelihood, util para evaluar modelo con psis loo
generated quantities {
vector[N] log_lik_D;
vector[N] log_lik_M;
for (i in 1:N)
log_lik_D[i] = normal_lpdf(D[i] | nu[i], tau);
for (i in 1:N)
log_lik_M[i] = normal_lpdf(M[i] | mu[i], sigma);
}