Mostrar / ocultar código
library(tidyverse) # pa 4 tontás de hacer sample y de groups bys que hago luego
library(parallel) # para usar varios cores con mclapply
library(patchwork) # pa juntar ggplotsJosé Luis Cañadas Reche
June 9, 2023
La gente de Yandex es gente lista y son los que están detrás de catboost. Ya el pasado mes de Abril conté como hacían la regresión cuantil y obtenían estimación de varios cuantiles a la vez aquí
Catboost por defecto usa one-hot-encoding pero si por algo es conocido es por tener otro método de codificación, el cual viene descrito en la docu. Otro sitio dónde viene relativamente bien explicado es en este post
Vamos a ver el detalle, para cuándo hay variables categóricas y la variable a predecir es binaria.
La idea en la que se basan tiene que ver con los test de permutación. Lo que hacen son varias iteraciones desordenando los datos y en cada iteración
Y luego para cada observación toman como codificación la media de las codificaciones obtenidas en las diferentes permutaciones.
En de la fila i se tiene que
countInClass: Cuenta las veces que en todos los datos previos a la fila i, se tiene un target = 1 para cuando el nivel de la variable categórica es igual al de la fila i.
prior: Constante que se define al principio del algoritmo. Puede ser la proporción de 1’s en los datos por ejemplo.
totalCount: El número de observaciones con el mismo nivel en la variable categórica que tiene la fila i, en los datos previos.
En el segundo post podemos ver la siguiente figura.
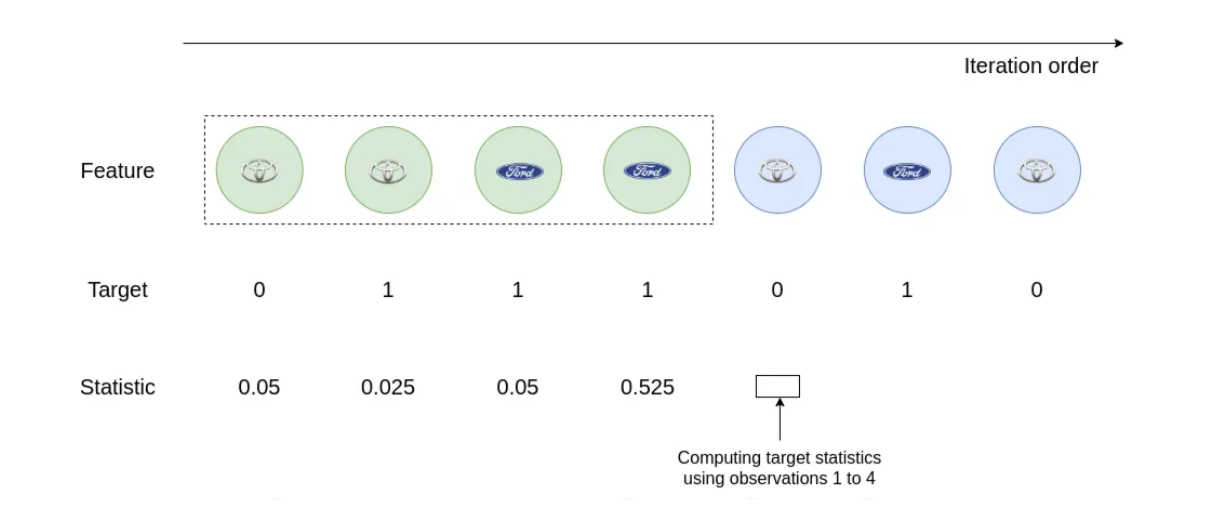
En este caso, si queremos calcular el valor de para la quinta observación es tan sencillo como
Así que
Los autores de catboost reconocen que de esta forma si sólo haces una permutación de los datos para los primeros valores no se tiene info suficiente para obtener una buena codificación, así que proponen hacer varias permutaciones y tomar como codificación la media de las codificaciones anteriores.
Pero, pero…
¿No os recuerda un poco a como se hace un aprendizaje bayesiano? . Es decir parto de una priori (puede que poco informativa) y conforme voy obteniendo datos voy actualizando la distribución de mi parámetro, y de esa forma puedo obtener la posterior predictive distribution, que es la que aplicaría por ejemplo a un dato no visto.
De hecho al hacer varias permutaciones ¿ no está convergiendo de alguna manera la solución de catboost hacia la aproximación bayesiana?
¿No os parece un poco de sobreingeniería, para algo que quizá con una aproximación estilo compadre bayesiana se podría obtener algo muy similar y con menos esfuerzo?
El ejemplo que viene en la docu, dónde se ejemplifica con un pequeño dataset de 7 filas y muestran una de las permutaciones generadas.
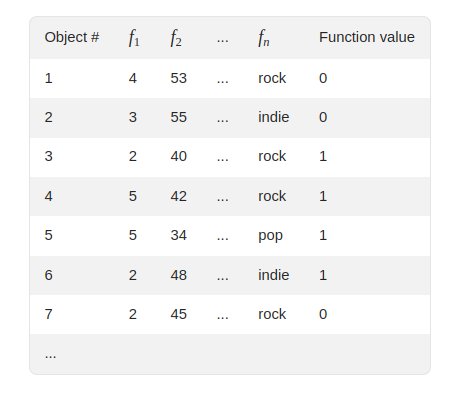
Que tras aplicar el algoritmo quedaría para esta permutación queda como 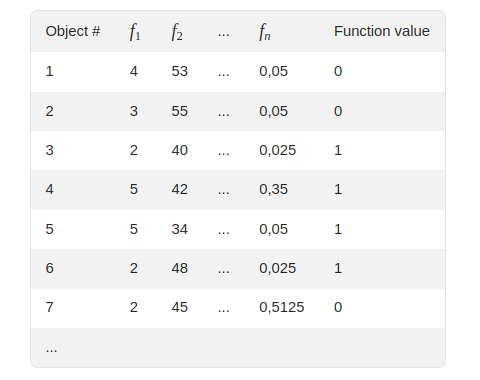
Replicamos en código
mydf <- tribble(
~id,~f2, ~cat, ~label,
1,53,"rock", 0,
2,55,"indie", 0,
3,40,"rock", 1,
4,42,"rock", 1,
5,34,"pop", 1,
6,48,"indie", 1,
7,45, "rock", 0
)
mydf
#> # A tibble: 7 × 4
#> id f2 cat label
#> <dbl> <dbl> <chr> <dbl>
#> 1 1 53 rock 0
#> 2 2 55 indie 0
#> 3 3 40 rock 1
#> 4 4 42 rock 1
#> 5 5 34 pop 1
#> 6 6 48 indie 1
#> 7 7 45 rock 0Funcioncita para obtener la codificación a lo catboost
A la primer fila se le asigna siempre la prior
Ahora lo repetimos varias veces. Dónde en cada iteración hacemos una permutación de las filas
foo2 <- function(df, prior = 0.05) {
require(tidyverse)
mynew_df <- df |> slice_sample(prop = 1, replace = FALSE)
mynew_df$cat_code[1] <- prior
for (fila in 2:nrow(mynew_df)) {
prev_df <- mynew_df[1:(fila - 1),]
mynew_df$cat_code[fila] <-
avg_target(prev_df = prev_df, nivel = mynew_df$cat[fila], prior = prior)
}
return(mynew_df)
}
iteraciones <- 1000
res2 <- bind_rows(mclapply(1:iteraciones, FUN = function(x) foo2(mydf,prior = 0.05), mc.cores = 10))
dim(res2)
#> [1] 7000 5
(res2 <- res2 |>
group_by(id) |>
mutate(cat_code = mean(cat_code)) |>
distinct() |>
arrange(id) )
#> # A tibble: 7 × 5
#> # Groups: id [7]
#> id f2 cat label cat_code
#> <dbl> <dbl> <chr> <dbl> <dbl>
#> 1 1 53 rock 0 0.340
#> 2 2 55 indie 0 0.284
#> 3 3 40 rock 1 0.175
#> 4 4 42 rock 1 0.194
#> 5 5 34 pop 1 0.05
#> 6 6 48 indie 1 0.0373
#> 7 7 45 rock 0 0.342¿Y si tomamos como priori una y para cada categoría {rock, indie, pop} tomamos como su distribución a posteriori
y para obtener un valor de la codificación para cada observación simplemente extraemos un valor aleatorio de esa distribución a posteriori?
res3 <- mydf |>
group_by(cat) |>
mutate(
n = n(),
exitos = sum(label)
) |>
ungroup() |>
mutate(
cat_code = map2_dbl(exitos, n, function(exitos, n) rbeta(1, exitos + 2 , n - exitos + 2))
)
res3
#> # A tibble: 7 × 7
#> id f2 cat label n exitos cat_code
#> <dbl> <dbl> <chr> <dbl> <int> <dbl> <dbl>
#> 1 1 53 rock 0 4 2 0.407
#> 2 2 55 indie 0 2 1 0.467
#> 3 3 40 rock 1 4 2 0.530
#> 4 4 42 rock 1 4 2 0.532
#> 5 5 34 pop 1 1 1 0.287
#> 6 6 48 indie 1 2 1 0.290
#> 7 7 45 rock 0 4 2 0.801Pues tiene pinta de que esta aproximación podría ser tan válida como la que describen los de catboost y en principio es más sencilla.
Creemos un dataset artificial partiendo de estos mismos datos.
n= 200
mydf_big= mydf[rep(seq_len(nrow(mydf)), n), ]
mydf_big$id <- 1:nrow(mydf_big)
nrow(mydf_big)
#> [1] 1400
head(mydf_big, 10)
#> # A tibble: 10 × 4
#> id f2 cat label
#> <int> <dbl> <chr> <dbl>
#> 1 1 53 rock 0
#> 2 2 55 indie 0
#> 3 3 40 rock 1
#> 4 4 42 rock 1
#> 5 5 34 pop 1
#> 6 6 48 indie 1
#> 7 7 45 rock 0
#> 8 8 53 rock 0
#> 9 9 55 indie 0
#> 10 10 40 rock 1## Cambiamos de forma aleatoria el valor de label para un % de las observaciones, para que no sea 200 veces exactamente el original
table(mydf_big$label)
#>
#> 0 1
#> 600 800
mydf_big$label <- rbinom(n = nrow(mydf_big), size =1, prob = ifelse(mydf_big$label==0, 0.3, 0.9))
table(mydf_big$label)
#>
#> 0 1
#> 508 892
# vemos que hemos cambiado algunos valores en label
head(mydf_big, 10)
#> # A tibble: 10 × 4
#> id f2 cat label
#> <int> <dbl> <chr> <int>
#> 1 1 53 rock 1
#> 2 2 55 indie 1
#> 3 3 40 rock 1
#> 4 4 42 rock 1
#> 5 5 34 pop 1
#> 6 6 48 indie 1
#> 7 7 45 rock 0
#> 8 8 53 rock 0
#> 9 9 55 indie 0
#> 10 10 40 rock 1Para elegir las priori poco informativa para ambos métodos vemos una muestra de los datos de tamaño 10
(muestra <- mydf_big |>
slice_sample(n = 10) |>
group_by(label) |>
count())
#> # A tibble: 2 × 2
#> # Groups: label [2]
#> label n
#> <int> <int>
#> 1 0 7
#> 2 1 3
(prior_shape1 <- muestra$n[muestra$label==1])
#> [1] 3
(prior_shape2 <- muestra$n[muestra$label==0])
#> [1] 7
(prior_catboost <- prior_shape1 /(prior_shape1 + prior_shape2))
#> [1] 0.3cod_catboost <- cod_catboost |>
group_by(id) |>
mutate(cat_code = mean(cat_code)) |>
distinct() |>
arrange(id)
dim(cod_catboost)
#> [1] 1400 5
head(cod_catboost)
#> # A tibble: 6 × 5
#> # Groups: id [6]
#> id f2 cat label cat_code
#> <int> <dbl> <chr> <int> <dbl>
#> 1 1 53 rock 1 0.587
#> 2 2 55 indie 1 0.567
#> 3 3 40 rock 1 0.577
#> 4 4 42 rock 1 0.586
#> 5 5 34 pop 1 0.910
#> 6 6 48 indie 1 0.582tictoc::tic("estilo compadre")
estilo_compadre <- mydf_big |>
group_by(cat) |>
mutate(
n = n(),
exitos = sum(label)
) |>
ungroup() |>
mutate(
cat_code = map2_dbl(exitos, n, function(exitos, n) rbeta(1, exitos + prior_shape1 , n - exitos + prior_shape2))
)
tictoc::toc(log = TRUE)
#> estilo compadre: 0.023 sec elapsed
head(estilo_compadre)
#> # A tibble: 6 × 7
#> id f2 cat label n exitos cat_code
#> <int> <dbl> <chr> <int> <int> <int> <dbl>
#> 1 1 53 rock 1 800 474 0.604
#> 2 2 55 indie 1 400 233 0.539
#> 3 3 40 rock 1 800 474 0.572
#> 4 4 42 rock 1 800 474 0.563
#> 5 5 34 pop 1 200 185 0.854
#> 6 6 48 indie 1 400 233 0.558¿cómo de parecidas son las dos codificaciones?
Por el momento parece que bastante
Parece que la codificación estilo compadre es un poco más dispersa, lo cual no tiene por qué ser necesariamente malo.
cod_catboost |>
group_by(cat) |>
summarise(media = mean(cat_code),
low = quantile(cat_code, 0.05),
high = quantile(cat_code, 0.95),
sd_value = sd(cat_code))
#> # A tibble: 3 × 5
#> cat media low high sd_value
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 indie 0.577 0.567 0.587 0.00635
#> 2 pop 0.906 0.888 0.916 0.00871
#> 3 rock 0.585 0.575 0.592 0.00520
estilo_compadre |>
group_by(cat) |>
summarise(media = mean(cat_code),
low = quantile(cat_code, 0.05),
high = quantile(cat_code, 0.95),
sd_value = sd(cat_code))
#> # A tibble: 3 × 5
#> cat media low high sd_value
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 indie 0.578 0.541 0.616 0.0240
#> 2 pop 0.896 0.857 0.933 0.0209
#> 3 rock 0.589 0.561 0.617 0.0173p1 <- cod_catboost |>
ggplot(aes(x=cat_code, fill=cat)) +
geom_density(alpha = 0.4) +
labs(title = "Gráfico densidad de las codificanes",
subtitle = "catboost")
p2 <- estilo_compadre |>
ggplot(aes(x=cat_code, fill=cat)) +
geom_density(alpha = 0.4) +
labs(title = "Gráfico densidad de las codificanes",
subtitle = "Estilo bayesian compadre")
p1 + p2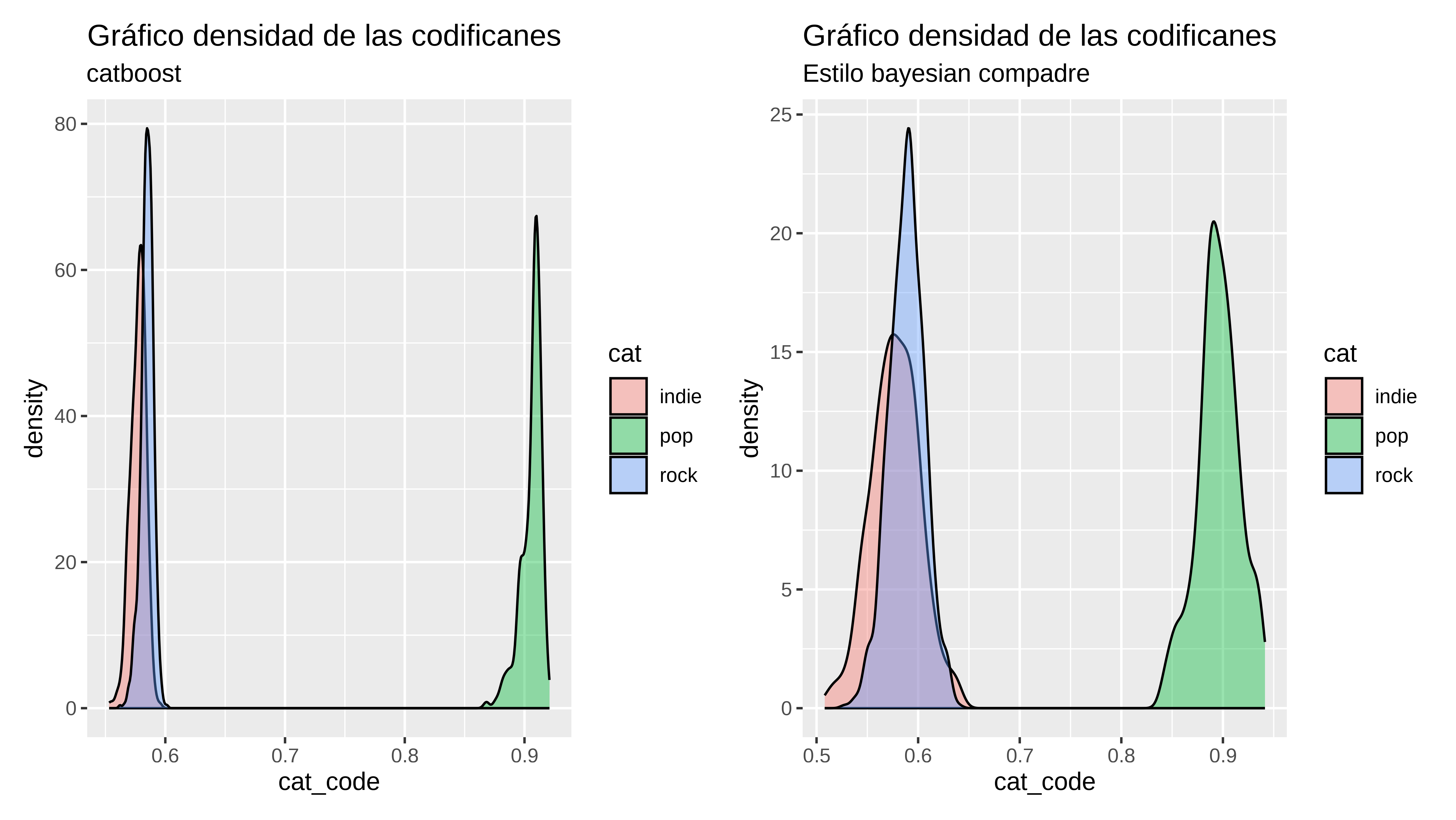
Y si hacemos un modelito tonto usando estas codificaciones. Si, ya sé que son datos fakes y que no tiene mucho sentido y tal, y que lo suyo sería con unos datos reales (mandadme algunos !! )
# set.seed(47)
id_train <- sample(1:nrow(mydf_big), size = 700)
train_predict_simple <- function(df){
train <- df[id_train, ]
test <- df[-id_train, ]
fit_base <- glm(label ~ f2+ cat, data = train, family = binomial)
fit <- glm(label ~ f2 + cat_code, data = train, family = binomial)
auc_base <- pROC::auc(test$label, predict(fit_base, test, type = "response"))
auc <- pROC::auc(test$label, predict(fit, test, type = "response"))
return(list(auc_base = auc_base, auc = auc))
}
mclapply(list(cod_catboost, estilo_compadre), train_predict_simple, mc.cores = 2)
#> [[1]]
#> [[1]]$auc_base
#> Area under the curve: 0.8231
#>
#> [[1]]$auc
#> Area under the curve: 0.7693
#>
#>
#> [[2]]
#> [[2]]$auc_base
#> Area under the curve: 0.8231
#>
#> [[2]]$auc
#> Area under the curve: 0.7658El ejemplo que he hecho no es del todo válido puesto que tanto para la codificación con catboost como la de estilo compadre han intervenido todos los datos.
La variable categórica que codifico sólo tiene 3 niveles, de hecho no haría falta hacer este tipo de codificación. Tengo pendiente probar con algo como códigos postales o similar.
La forma en que catboost hace esta codificación me parece que está en mitad entre la aproximación bayesiana y hacer un target_encoding al uso. De hecho si hay un nivel con muy pocos valores el valor de la codificación de catboost para ese nivel va a parecerse más a la prior que elijas que a la proporción de éxitos en esa categoría, lo cual es muy parecido a la estimación bayesiana compadre.
Se podrían utilizar codificaciones basadas en modelos mixtos o algún tipo de combinación convexa entre la información particular que tiene una categoría y la general aportada por el conjunto de los datos.