MMM. Estilo compadre

Listening

Confesión

He de reconocer que mi conocimiento sobre lo que se ha dado en llamar el Marketing/Media Mix Modelling es más bien escaso por no decir que inexistente. No obstante, una reunión el otro día en el trabajo hizo despertar mi curiosidad. Así que voy a contar un poco lo que he aprendido.

Qué es esto del marketing mix modelling.

Pues en teoría es un intento de inferencia causal, que intenta responder a la pregunta de ¿qué pasa con las ventas si aumento mi inversión publicitaria en un canal a ? ¿ Y si cambio por completo el mix de gasto en publicidad? ¿Si tengo un presupuesto Z, cuál es la forma óptima de asignar gasto a cada medio?

Bien, pues para poder contestar a estas preguntas lo primero de todo es asumir que las ventas están relacionadas e incluso son causa de la inversión en publicidad. Suena a palabras mayores, desde luego, pero que le vamos a hacer, esto es lo que hay.

Uno podría (y debería) pintar un DAG que expresase lo que creemos saber sobre la relación entre las variables. Quizá el gasto en radio influya en que el gasto en google sea más eficaz, y cosas así. Pero como yo estoy empezando a aprender sobre este tema, voy a partir del supuesto, de que una regresión múltiple me permite expresar las relaciones causales entre las variables, y además que se dan todo el resto de supuestos para la inferencia causal y por tanto, podría interpretar los coeficientes como efectos causales. Si, ya lo sé, esto es un triple salto mortal, pero es lo que se hace todos los días en las empresas. Ya habrá tiempo de cuestionar estas cosas.

Unos datillos de ejemplo

En la librería datarium tenemos unos datos de marketing que nos pueden servir

library(datarium)

datos  <- marketing

Estos datos son muy sencillos, son 200 filas y 4 columnas que se corresponden con la inversión publicitaria en 3 canales (youtube, facebook, newspaper) y una última columna con el monto de las ventas.

dim(datos)
#> [1] 200   4
head(datos)
#>   youtube facebook newspaper sales
#> 1  276.12    45.36     83.04 26.52
#> 2   53.40    47.16     54.12 12.48
#> 3   20.64    55.08     83.16 11.16
#> 4  181.80    49.56     70.20 22.20
#> 5  216.96    12.96     70.08 15.48
#> 6   10.44    58.68     90.00  8.64

Leyendo la documentación sobre este conjunto de datos se podría asumir que los datos están ordenados por fechas, voy a suponer que cada fila corresponde a una semana, así que voy a pegar una variable de semana y otra que sea simplemente del 1 al 200.

datos$fecha_arbitraria <- seq.Date(as.Date("2020-01-02"), length.out =200, by = "week")
datos$semana <- lubridate::week(datos$fecha_arbitraria)
datos$time <- 1:200

datos$mes <- lubridate::month(datos$fecha_arbitraria)
datos$anyo <- lubridate::year(datos$fecha_arbitraria)

head(datos)
#>   youtube facebook newspaper sales fecha_arbitraria semana time mes anyo
#> 1  276.12    45.36     83.04 26.52       2020-01-02      1    1   1 2020
#> 2   53.40    47.16     54.12 12.48       2020-01-09      2    2   1 2020
#> 3   20.64    55.08     83.16 11.16       2020-01-16      3    3   1 2020
#> 4  181.80    49.56     70.20 22.20       2020-01-23      4    4   1 2020
#> 5  216.96    12.96     70.08 15.48       2020-01-30      5    5   1 2020
#> 6   10.44    58.68     90.00  8.64       2020-02-06      6    6   2 2020

Pintamos

library(tidyverse)

datos  %>%
  ggplot(aes(fecha_arbitraria, sales)) +
  geom_point() + 
  geom_line()

Teoría marketiniana

En estas cosas de marketing mix modelling hay algunas cosillas peculiares. La primera es que se asume, y no me parece mal, que en un instante t la inversión publicitaria que “causa” las ventas no es sólo la del instante t sino que también hay cierto efecto “remanente” de la inversión pasada. Y por tanto en vez de considerar la variable tal cual en un instante t se considera algo como

\[ X_{Adstock} = X_t + \lambda_{1} \times X_{t-1} + ...\lambda_{n} \times X_{t-n} \]

pero además vamos a poner un período de olvido de 2 .

En R podemos hacerlo de la siguiente forma. Por ejemplo para facebook

Se supone que los datos están ordenados de fecha más antigua a más reciente. El criterio de poner set_rate_fb = 0.1 ha sido arbitrario, pero se podría estimar.

#set adstock fb rate
set_rate_fb <- 0.1
set_memory <- 2
get_adstock_fb <- rep(set_rate_fb, set_memory+1) ^ c(0:set_memory)

ads_fb <- stats::filter(c(rep(0, set_memory), datos$facebook), get_adstock_fb, method="convolution")
ads_fb <- ads_fb[!is.na(ads_fb)]

head(datos$facebook)
#> [1] 45.36 47.16 55.08 49.56 12.96 58.68
head(ads_fb)
#> [1] 45.3600 51.6960 60.2496 55.5396 18.4668 60.4716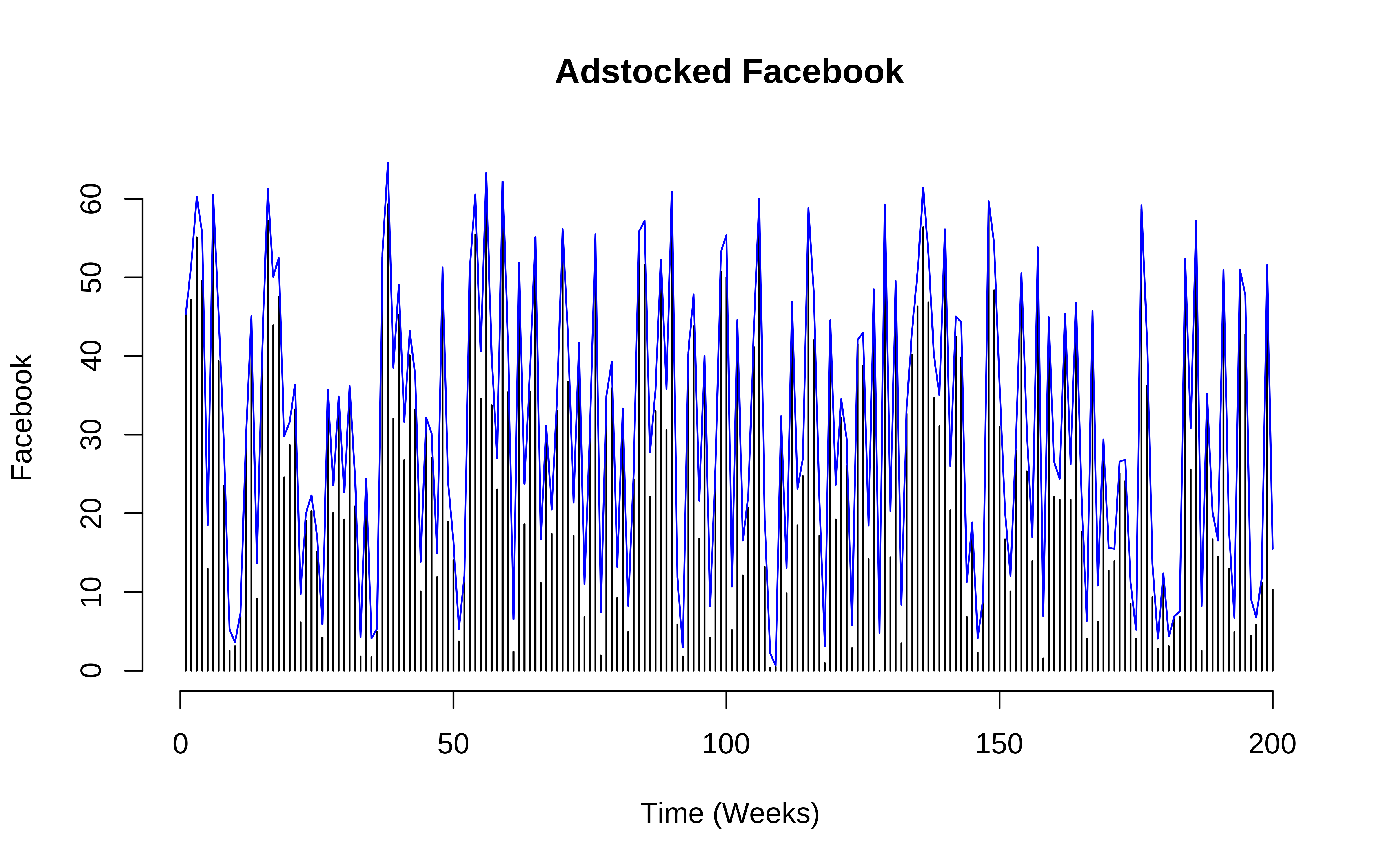

plot(seq(1,length(datos$facebook)), datos$facebook, type="h", 
     main = "Adstocked Facebook",
     xlab="Time (Weeks)", ylab="Facebook", 
     ylim=c(0, max(c(datos$facebook, ads_fb))), 
     frame.plot=FALSE)
lines(ads_fb, col="blue")

Hacemos lo mismo para resto de canales, con diferente valor

#set adstock youtube rate
set_rate_yt <- 0.15
set_memory <- 2
get_adstock_youtube <- rep(set_rate_yt, set_memory+1) ^ c(0:set_memory)

#set adstock news rate
set_rate_news <- 0.25
set_memory <- 2
get_adstock_news <- rep(set_rate_news, set_memory+1) ^ c(0:set_memory)


ads_youtube <- stats::filter(c(rep(0, set_memory), datos$youtube), get_adstock_youtube, method="convolution")
ads_youtube <- ads_youtube[!is.na(ads_youtube)]

#adstocked newpaper
ads_news <- stats::filter(c(rep(0, set_memory), datos$newspaper), get_adstock_news, method="convolution")
ads_news <- ads_news[!is.na(ads_news)]
#plot


datos <- cbind(datos, ads_fb, ads_youtube, ads_news)
head(datos)
#>   youtube facebook newspaper sales fecha_arbitraria semana time mes anyo
#> 1  276.12    45.36     83.04 26.52       2020-01-02      1    1   1 2020
#> 2   53.40    47.16     54.12 12.48       2020-01-09      2    2   1 2020
#> 3   20.64    55.08     83.16 11.16       2020-01-16      3    3   1 2020
#> 4  181.80    49.56     70.20 22.20       2020-01-23      4    4   1 2020
#> 5  216.96    12.96     70.08 15.48       2020-01-30      5    5   1 2020
#> 6   10.44    58.68     90.00  8.64       2020-02-06      6    6   2 2020
#>    ads_fb ads_youtube ads_news
#> 1 45.3600    276.1200  83.0400
#> 2 51.6960     94.8180  74.8800
#> 3 60.2496     34.8627 101.8800
#> 4 55.5396    186.0975  94.3725
#> 5 18.4668    244.6944  92.8275
#> 6 60.4716     47.0745 111.9075

Modelando

Pues en esta primera parte de MMM estilo compadre se trata simplemente de estimar las ventas en base al tiempo y al adstock, es decir, un ejercicio de estimación de series temporales. De hecho, las consultoras que se dedican a estos temas hacen una serie de modelos lineales, a veces encadenados (y sin ajustar conjuntamente, lo cual es un error importante), y algunas asumen modelos lineales sin Intercept , es decir, tienen la asunción fuerte (y errónea) que todas las ventas se deben exclusivamente a variables modeladas y que a inversión 0, las ventas no existen. Yo no voy a asumir semejante cosa, dios me libre.

Primer modelo sencillito

Pues ya que el software lo permite, vamos a hacer un modelito, pero bayesiano.

library(cmdstanr)
library(brms)

En vez de modelar las ventas , modelo su logaritmo neperiano, por qué? porque me da la gana, y porque a veces así se consiguen mejores resultados. En realidad habría que probar ambas cosas. De hecho, quizá sea mejor modelar las ventas en vez del log(ventas) en aras a la interpretabilidad de los parámetros. Podéis probar, yo ya lo voy a dejar con logaritmo.

También meto un término de splines, y entreno con los primeros 150 datos y dejo de test los últimos 50

train <- datos[1:150, ]
test <-  datos[151:200, ]


mod_splines <- brm(log(sales) ~ ads_fb + ads_youtube + ads_news  + s(time, k = 10),
              data = train,
              family = gaussian(),
              backend = "cmdstanr",
              cores = 4,
              file = here::here("2024/06/mod_splines") )

summary(mod_splines)
#>  Family: gaussian 
#>   Links: mu = identity; sigma = identity 
#> Formula: log(sales) ~ ads_fb + ads_youtube + ads_news + s(time, k = 10) 
#>    Data: train (Number of observations: 150) 
#>   Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
#>          total post-warmup draws = 4000
#> 
#> Smoothing Spline Hyperparameters:
#>              Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sds(stime_1)     0.24      0.25     0.01     0.92 1.00      873     1522
#> 
#> Regression Coefficients:
#>             Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept       1.82      0.05     1.72     1.92 1.00     4112     3263
#> ads_fb          0.01      0.00     0.01     0.01 1.00     4291     2309
#> ads_youtube     0.00      0.00     0.00     0.00 1.00     3771     2568
#> ads_news        0.00      0.00    -0.00     0.00 1.00     4136     2779
#> stime_1         0.07      0.53    -0.84     1.43 1.00     1088      808
#> 
#> Further Distributional Parameters:
#>       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sigma     0.20      0.01     0.18     0.23 1.00     3608     3041
#> 
#> Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

Algún chequeo del modelo

Uno de los chequeos básico es comparar la variable respuesta en los datos con la que genera el modelo.

Se pinta la variable real y las generadas mediante la posterior predictive . Vamos a pintar 100 posteriors

pp_check(mod_splines, ndraws  = 100)

y no tiene mala pinta.

Veamos como predice el modelo para los datos de test.

predicciones <- posterior_predict(mod_splines, newdata = test, ndraws = 1000)
predicciones_medias <- apply(predicciones, 2, mean)

test$ventas_predichas <- exp(predicciones_medias)

Vemos alguna métrica como el RMSE o el MAE

yardstick::rmse(test, sales, ventas_predichas)
#> # A tibble: 1 × 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        2.45
yardstick::mae(test, sales, ventas_predichas)
#> # A tibble: 1 × 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 mae     standard        1.91

Pintamos las ventas predicas vs las reales en test, para ver si caen cerca de la recta \(y = x\)

test  %>%
  ggplot(aes(x = ventas_predichas, y = sales)) +
  geom_point()  +
  geom_smooth(method ="lm", linetype = "dashed") +
  geom_abline(intercept = 0, slope = 1)

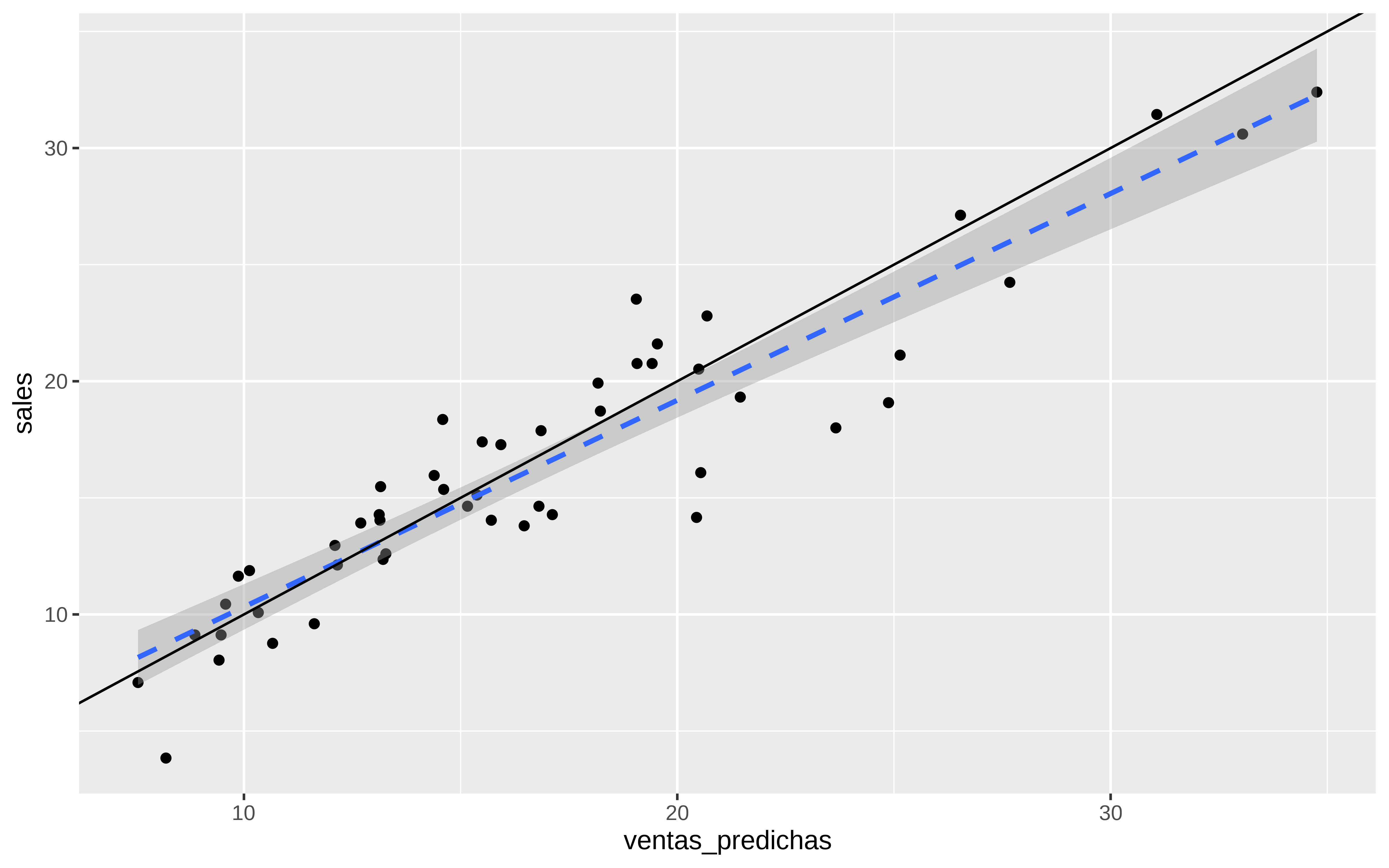
Y bueno, ni tan mal.

Optimizando

Pues el tema en esto del MMM consiste ahora en encontrar cuánto hay que invertir en cada canal para optimizar las ventas , pero sujeto a unas restricciones, por ejemplo presupuestarias.

Todo esto con la asunción de que el modelo ajustado representa la verdadera relación causal y no sólo asociación.

El principal problema que yo veo a estas cosas es que si yo he entrenado con un rango de gasto histórico en un canal A, el modelo puede haber estimado que a más gasto más ventas y extrapolar mucho más allá de lo aconsejable.

Lo primero es crear una función que simule las ventas obtenidas.

Suponemos que nuestros nuevos datos irán temporalmente detrás de los datos de train, y que por tanto el adstock se ve influido por datos antiguos

simular_ventas_siguiente_periodo <- function(facebook_new, youtube_new, news_new,  modelo) {
 
  nuevo_time = max(train$time) + 1
  
  # obtener add_stock 
  ads_fb <- stats::filter(c(rep(0, set_memory), train$facebook, facebook_new), get_adstock_fb, method="convolution")
  ads_fb <- ads_fb[!is.na(ads_fb)]
  ads_fb <-  tail(ads_fb, 1)
  
  
  ads_youtube <- stats::filter(c(rep(0, set_memory), train$youtube, youtube_new), get_adstock_youtube, method="convolution")
  ads_youtube <- ads_youtube[!is.na(ads_youtube)]
  ads_youtube <-  tail(ads_youtube, 1)
  
  
  ads_news <- stats::filter(c(rep(0, set_memory), train$newspaper, news_new), get_adstock_news, method="convolution")
  ads_news <- ads_news[!is.na(ads_news)]
  ads_news <-  tail(ads_news, 1)
  
  newdata = data.frame(ads_fb = ads_fb, ads_youtube = ads_youtube, ads_news = ads_news, time = nuevo_time)
  
 # estimamos con el modelo  
  ventas_simuladas <- posterior_predict(modelo, newdata = newdata, ndraws = 500)
 
  return(as.numeric(ventas_simuladas))
}

La probamos, incrementando en 1% la media de gasto en cada canal que se ha visto en los datos de entrenamiento

facebook_new <-  mean(train$facebook) * 1.01
youtube_new <-  mean(train$youtube) * 1.01
news_new <-  mean(train$newspaper) * 1.01

# Obtenemos la posteriori, teniendo en cuenta el adstock.

simulaciones <- simular_ventas_siguiente_periodo(facebook_new, youtube_new, news_new,  mod_splines)

simulaciones %>% 
  as_tibble() %>% 
  ggplot(aes(x = exp(value))) +
  geom_density() +
  labs(title = "Distribución de ventas esperadas",
       x = "Ventas esperadas",
       y = "Densidad") +
  theme_minimal()

Una observación

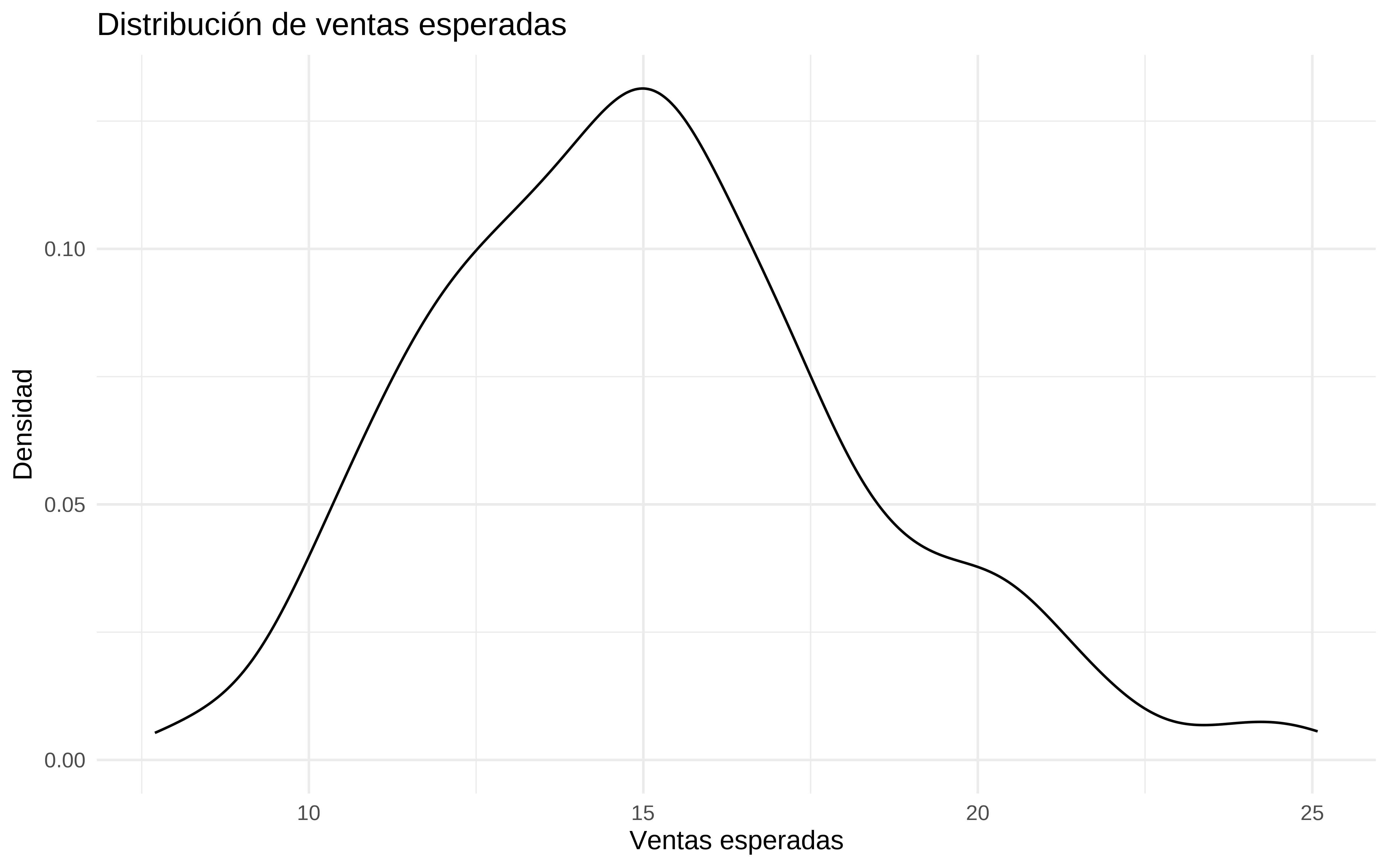
Al haber modelado el log de las ventas, la interpretación de los parámetros ya no es tan directa, pero podemos utilizar la función de simular ventas para hacer análisis de sensibilidad y contestar a qué pasa si varío las cosas de tal o cual manera. Esto es relativamente simple y puede aportar más valor que incluso la optimización, puesto que permite al usuario jugar con cuánto invertir en cada medio. Y en cierta forma sentirse realizado, aún cuando , como he advertido la relación causal esté sólo en su imaginación.

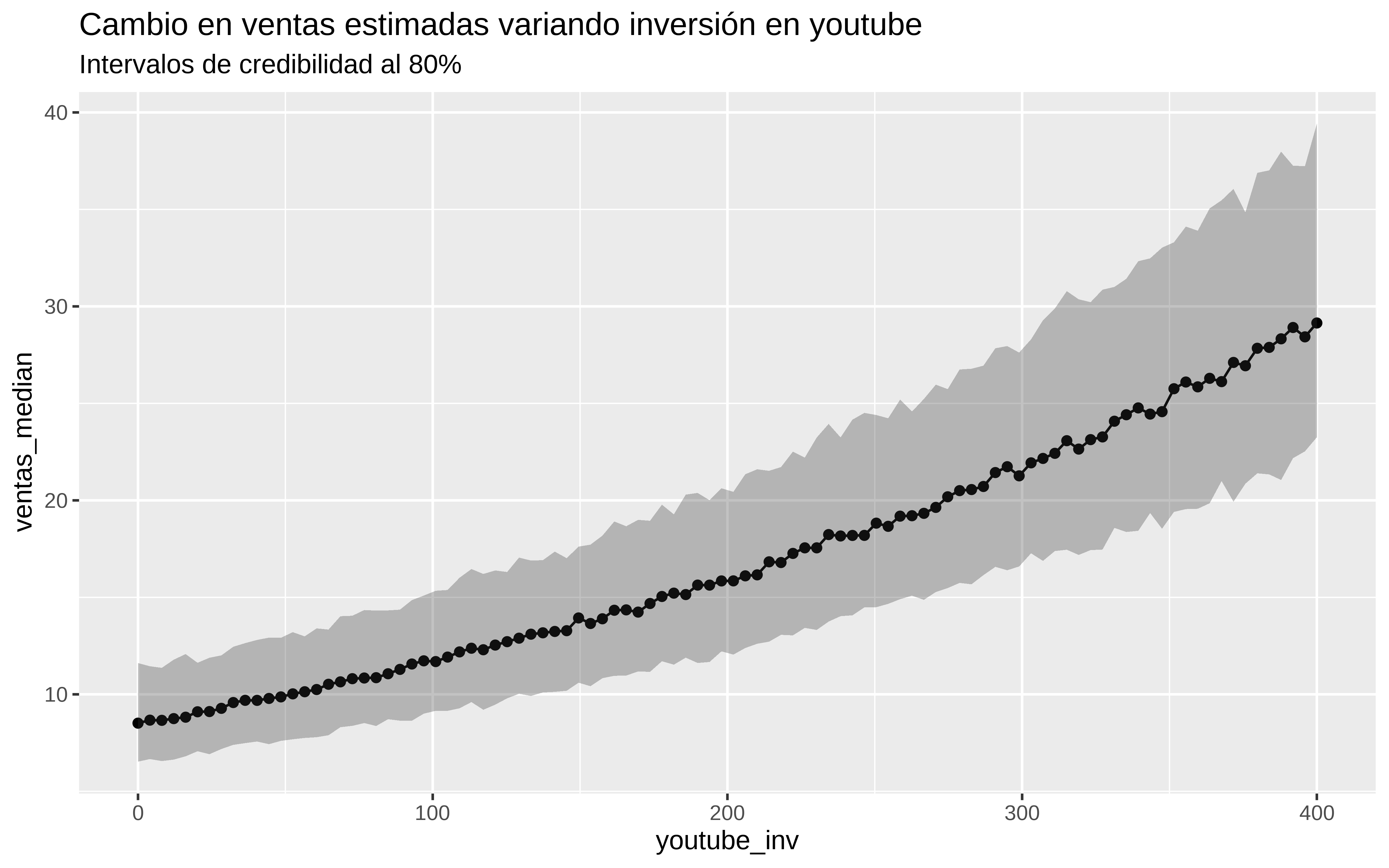
Dejamos los valores de inversión en facebook y news como la media vista en train y variamos la inversión en youtube.

facebook_mean = mean(train$facebook)
news_mean = mean(train$newspaper)
youtube_grid = seq(0, 400, length.out = 100)

simular_ventas_grid_youtube  <-  partial(simular_ventas_siguiente_periodo, facebook_new = facebook_mean, 
news_new = news_mean, modelo = mod_splines)
sim_grid_youtube <- youtube_grid  %>% map(simular_ventas_grid_youtube)

# sumarizo las 100 posteriors por su mediana, por simpliciddad

sim_grid_youtube_medians <- sim_grid_youtube  %>% map_dbl(median)
sim_grid_youtube_means <- sim_grid_youtube  %>% map_dbl(mean)
sim_grid_youtube_low <- sim_grid_youtube  %>% map_dbl(quantile, probs = 0.1)
sim_grid_youtube_high <- sim_grid_youtube  %>% map_dbl(quantile, probs = 0.9)

to_plot <- data.frame(youtube_inv = youtube_grid,
                      ventas_median = exp(sim_grid_youtube_medians),
                      ventas_low = exp(sim_grid_youtube_low),
                      ventas_high = exp(sim_grid_youtube_high)
                      )

to_plot %>%
  ggplot(aes(x = youtube_inv, y = ventas_median)) +
  geom_point() +
  geom_line() +
  geom_ribbon(aes(ymin = ventas_low, ymax = ventas_high), alpha = 0.3) +
  labs(
       title = "Cambio en ventas estimadas variando inversión en youtube",
       subtitle = "Intervalos de credibilidad al 80%"
  )

Volvamos a la optimización

Bien, pues ahora tenemos que construir la función a optimizar. Vamos a poner un presupuesto máximo de 450. Y en la función a optimizar añadimos una penalización alta si la suma de los valores a optimizar supera este presupuesto. Aparte de este valor máximo también vamos a poner umbrales al valor mínimo y máximo del gasto en cada canal.

funcion_objetivo <- function(facebook_new, youtube_new, news_new, modelo, presupuesto = 450) {
  
  penalizacion <- 0
  
  # Calcular la suma de los parámetros
  suma_par <- sum(facebook_new, youtube_new, news_new)
  
  # Si la suma de los parámetros supera el presupuesto, añadir una penalización
  if (suma_par > presupuesto) {
    penalizacion <- 1e6 * (suma_par - presupuesto)^2
  }
  
  ventas_simuladas <- simular_ventas_siguiente_periodo(facebook_new, youtube_new, news_new, modelo)
  
  # para optimizar necesitamos un solo valor, no las posteriores, sumarizamos con la media, pero podría 
  # ser otra cosa

  ventas_esperadas <- mean(ventas_simuladas)
  return(list(Score = -ventas_esperadas + penalizacion)) # Negativo para maximizar
}

(prueba <- funcion_objetivo(facebook_new, youtube_new, news_new, modelo= mod_splines))
#> $Score
#> [1] -2.700242

# las ventas serán el exp de menos el resultado
exp(-prueba$Score)
#> [1] 14.88333

Ahora sería optimizar esa función con algún solver, yo voy a usar una optimización bayesiana y en procesamiento paralelo

library(ParBayesianOptimization)
library(doParallel)
library(foreach)

# Configurar el clúster para usar 5 núcleos

num_cores <- 5
cl <- makeCluster(num_cores)
registerDoParallel(cl)

Límites de gasto. ¿Por qué pongo estos? Porque quiero, y he añadido que el mínimo en news sea 13

bounds <- list(
    facebook_new = c(0, 224)
  , youtube_new = c(0, 400)
  , news_new = c(13, 34)
)

Me creo una función parcial para rellenar por defecto algunos parámetros de la función como el modelo a usar y el presupuesto. Esto lo hago porque muchas veces los solvers requieren quela función objetivo tenga sólo un argumento.

# Aquí pongo un presupuesto máximo de 500
f_objetivo_partial  <- partial(funcion_objetivo, modelo = mod_splines, presupuesto = 500)
f_objetivo_partial
#> <partialised>
#> function (...) 
#> funcion_objetivo(modelo = mod_splines, presupuesto = 500, ...)

Para hacer la computación en paralelo hay que copiar las librerías y los datos y funciones en cada “conexión”, al menos para usar esta librería

Las librerías hay que enviarlas a cada proceso de R con clusterEvalQ y las funciones y datos usados con clusterExport. Seguro que hay una forma de no mandar una copia de los datos a cada proceso, y lo he hecho alguna vez, pero no recuerdo como.

clusterEvalQ(cl, {
  library(ParBayesianOptimization)
  library(tidyverse)
  library(brms)
  })
#> [[1]]
#>  [1] "brms"                    "Rcpp"                   
#>  [3] "lubridate"               "forcats"                
#>  [5] "stringr"                 "dplyr"                  
#>  [7] "purrr"                   "readr"                  
#>  [9] "tidyr"                   "tibble"                 
#> [11] "ggplot2"                 "tidyverse"              
#> [13] "ParBayesianOptimization" "stats"                  
#> [15] "graphics"                "grDevices"              
#> [17] "utils"                   "datasets"               
#> [19] "methods"                 "base"                   
#> 
#> [[2]]
#>  [1] "brms"                    "Rcpp"                   
#>  [3] "lubridate"               "forcats"                
#>  [5] "stringr"                 "dplyr"                  
#>  [7] "purrr"                   "readr"                  
#>  [9] "tidyr"                   "tibble"                 
#> [11] "ggplot2"                 "tidyverse"              
#> [13] "ParBayesianOptimization" "stats"                  
#> [15] "graphics"                "grDevices"              
#> [17] "utils"                   "datasets"               
#> [19] "methods"                 "base"                   
#> 
#> [[3]]
#>  [1] "brms"                    "Rcpp"                   
#>  [3] "lubridate"               "forcats"                
#>  [5] "stringr"                 "dplyr"                  
#>  [7] "purrr"                   "readr"                  
#>  [9] "tidyr"                   "tibble"                 
#> [11] "ggplot2"                 "tidyverse"              
#> [13] "ParBayesianOptimization" "stats"                  
#> [15] "graphics"                "grDevices"              
#> [17] "utils"                   "datasets"               
#> [19] "methods"                 "base"                   
#> 
#> [[4]]
#>  [1] "brms"                    "Rcpp"                   
#>  [3] "lubridate"               "forcats"                
#>  [5] "stringr"                 "dplyr"                  
#>  [7] "purrr"                   "readr"                  
#>  [9] "tidyr"                   "tibble"                 
#> [11] "ggplot2"                 "tidyverse"              
#> [13] "ParBayesianOptimization" "stats"                  
#> [15] "graphics"                "grDevices"              
#> [17] "utils"                   "datasets"               
#> [19] "methods"                 "base"                   
#> 
#> [[5]]
#>  [1] "brms"                    "Rcpp"                   
#>  [3] "lubridate"               "forcats"                
#>  [5] "stringr"                 "dplyr"                  
#>  [7] "purrr"                   "readr"                  
#>  [9] "tidyr"                   "tibble"                 
#> [11] "ggplot2"                 "tidyverse"              
#> [13] "ParBayesianOptimization" "stats"                  
#> [15] "graphics"                "grDevices"              
#> [17] "utils"                   "datasets"               
#> [19] "methods"                 "base"
  
  
  
clusterExport(cl,c('simular_ventas_siguiente_periodo', 'train','bounds', 'funcion_objetivo','f_objetivo_partial', 'mod_splines', 
                   'set_memory', 'get_adstock_fb', 'get_adstock_youtube', 
                   'get_adstock_news'))

Y ya podríamos optimizar. He puesto un máximo de 200 iteraciones y un tiempo máximo de 300 segundos. Para ver más opciones consultar la ayuda de la función, que hace optimización usando procesos gaussianos

bayes_opt <- bayesOpt(
  FUN = f_objetivo_partial,
  bounds = bounds,
  initPoints = 10,
  acq = "ei",
  iters.n = 200,
  iters.k = 10,
  kappa = 2,
  eps = 0.0, 
  parallel = TRUE,
  otherHalting = list(timeLimit = 300)
)

Y los resultados los podemos ver ordenando por Score, el mejor resultado será el que tenga menor Scores (estamos minimizando )

# Mostrar los resultados
print(bayes_opt)
#> Class: bayesOpt
#> 
#>                     Epochs: 15
#>                 Iterations: 168
#>        Average FUN Seconds: 0.51
#>        Highest FUN Seconds: 0.73
#> Final Expected Improvement: 0.5197976
#>                 GP Updated: FALSE
#>                Stop Status: Stopped Early. See $stopStatus
bayes_opt$scoreSummary %>% 
  arrange(Score) 
#>      Epoch Iteration facebook_new youtube_new news_new gpUtility acqOptimum
#>      <num>     <int>        <num>       <num>    <num>     <num>     <lgcl>
#>   1:     0         7     202.9549    176.0488 15.10575        NA      FALSE
#>   2:     0         8     168.9526    243.1588 21.22847        NA      FALSE
#>   3:     0         6     132.1047    346.3188 18.72091        NA      FALSE
#>   4:     0         9     101.5759    363.3885 24.58786        NA      FALSE
#>   5:     0         3     198.6377     53.1898 14.67486        NA      FALSE
#>  ---                                                                       
#> 164:    15       158     217.7454    400.0000 32.30452 0.4272278      FALSE
#> 165:    15       154     224.0000    392.5891 34.00000 0.3830230      FALSE
#> 166:    15       157     224.0000    400.0000 32.03328 0.4884866      FALSE
#> 167:    15       152     224.0000    400.0000 32.30285 0.4930121      FALSE
#> 168:    15       151     224.0000    400.0000 34.00000 0.5197976       TRUE
#>      inBounds Elapsed         Score errorMessage
#>        <lgcl>   <num>         <num>       <lgcl>
#>   1:     TRUE   0.450 -4.285181e+00           NA
#>   2:     TRUE   0.578 -4.171461e+00           NA
#>   3:     TRUE   0.405 -4.157552e+00           NA
#>   4:     TRUE   0.647 -3.955043e+00           NA
#>   5:     TRUE   0.675 -3.877969e+00           NA
#>  ---                                            
#> 164:     TRUE   0.576  2.251499e+10           NA
#> 165:     TRUE   0.410  2.267709e+10           NA
#> 166:     TRUE   0.395  2.434638e+10           NA
#> 167:     TRUE   0.529  2.443058e+10           NA
#> 168:     TRUE   0.545  2.496400e+10           NA

Los valores óptimos que ha encontrado de gasto en cada canal, cumpliendo las restricciones

(result_bayes <- bayes_opt$scoreSummary %>% 
 arrange(Score) %>% 
 head(1) %>% 
 select(facebook_new, youtube_new, news_new, Score) )
#>    facebook_new youtube_new news_new     Score
#>           <num>       <num>    <num>     <num>
#> 1:     202.9549    176.0488 15.10575 -4.285181

Comprobamos que no se ha pasdo del presupuesto

with(result_bayes, sum(facebook_new, youtube_new, news_new))
#> [1] 394.1095

Simulamos las ventas que se esperan con esta optimización.

simulaciones_optim <- simular_ventas_siguiente_periodo(result_bayes$facebook_new, result_bayes$youtube_new, result_bayes$news_new,
                                                       modelo = mod_splines)
exp(quantile(simulaciones_optim, c(0.2, 0.5, 0.8)))
#>      20%      50%      80% 
#> 57.90940 73.23327 90.95111

(p_optimizacion_mod_spline <- simulaciones_optim %>% 
  as_tibble() %>% 
  ggplot(aes(x = exp(value))) +
  geom_density() +
  labs(title = "Distribución de ventas esperadas tras optimización",
       subtitle = "Modelo simple con splines",
       x = "Ventas esperadas",
       y = "Densidad") +
  theme_minimal())

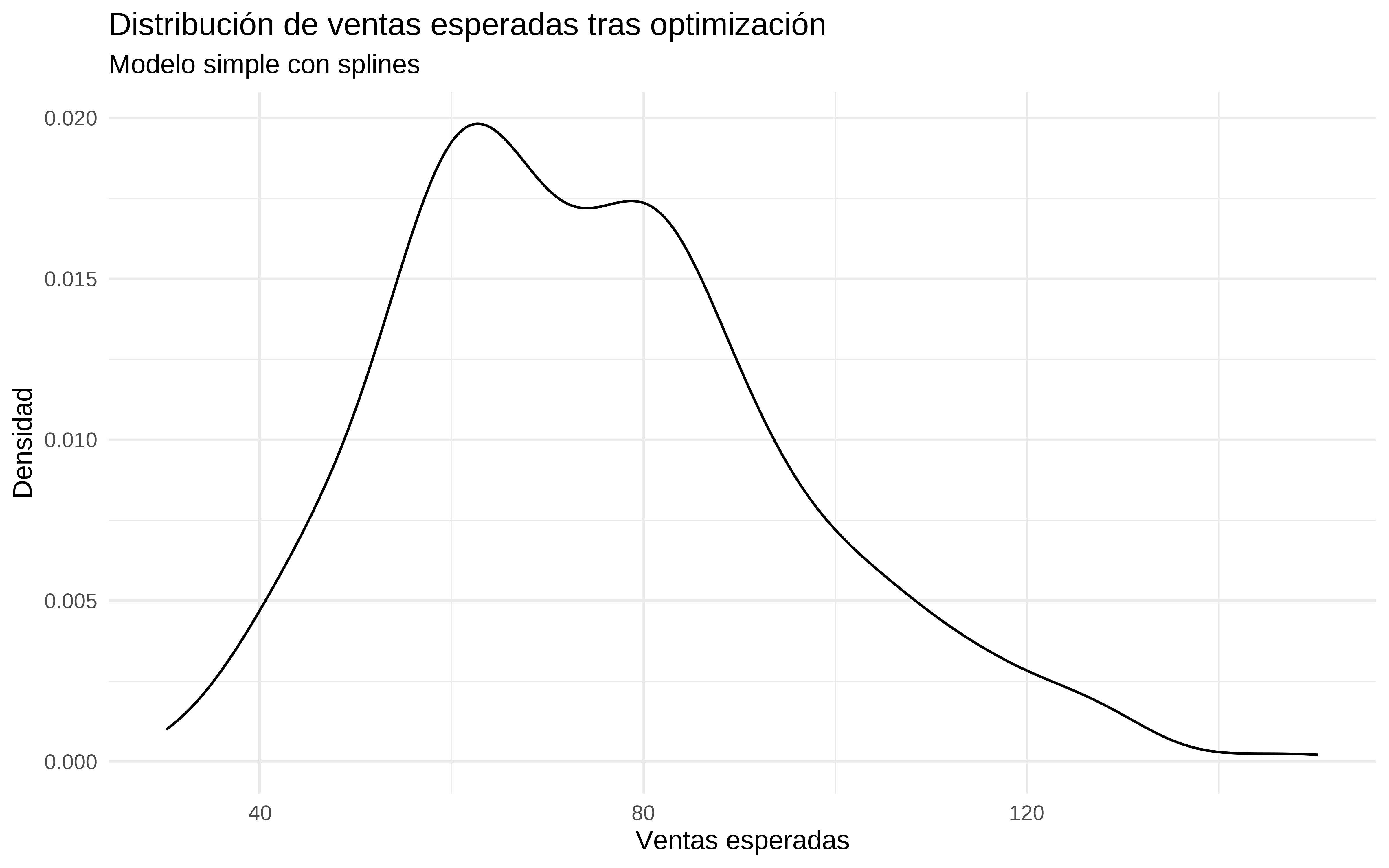
Y básicamente esta sería la idea principal de hacer un MMM.

Curvas de saturación y como modelarlas

Sin embargo también se considera el concepto de curva de saturación, que no es más que la asunción de que llega un momento en que por más que te gastes en publicidad, no vas a tener más ventas.

Por ejemplo, para eso veamos si eso se ve en los datos

Con los datos reales y gastos en youtube se intuye que podría existir más allá del dominio observado de la variable.

(p_youtube_real <- datos %>% 
  group_by(ads_youtube) %>%
  summarise(ventas_mean = mean(log(sales))) %>%
  ggplot(aes(x = ads_youtube, y = ventas_mean)) +
  geom_point() +
  geom_smooth() +
  scale_x_continuous(limits = c(0, 450)) +
  scale_y_continuous(limits = c(0, 4)) +
  labs(title = "Curva real en los datos",
       x = "Gasto en youtube",
       y = "Ventas, en log"))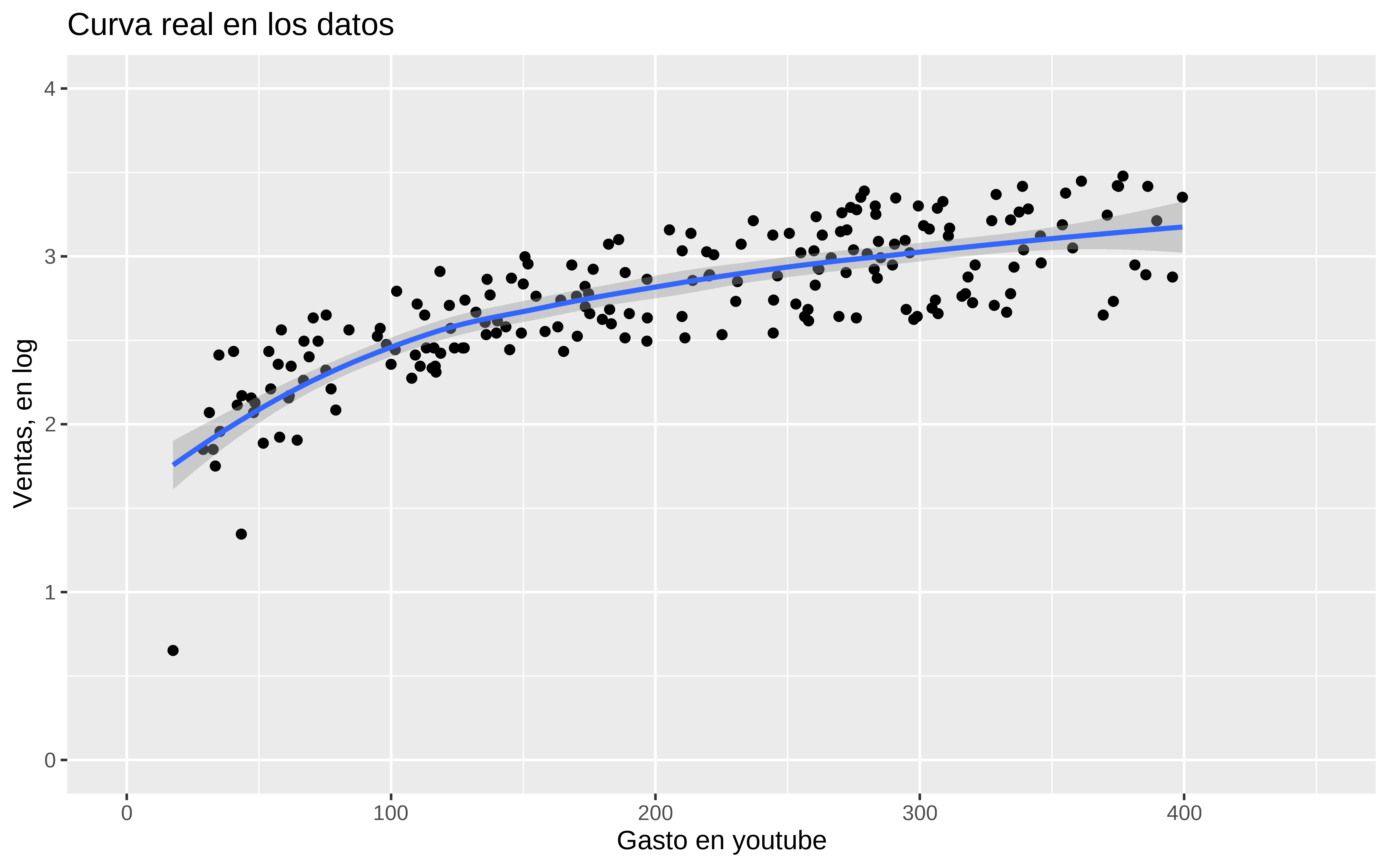

(p_facebook_real <- datos %>% 
  group_by(ads_fb) %>%
  summarise(ventas_mean = mean(log(sales))) %>%
  ggplot(aes(x = ads_fb, y = ventas_mean)) +
  geom_point() +
  geom_smooth() +
  scale_x_continuous(limits = c(0, 100)) +
  scale_y_continuous(limits = c(0, 4)) +
  labs(title = "Curva real en los datos",
       x = "Gasto en facebook",
       y = "Ventas"))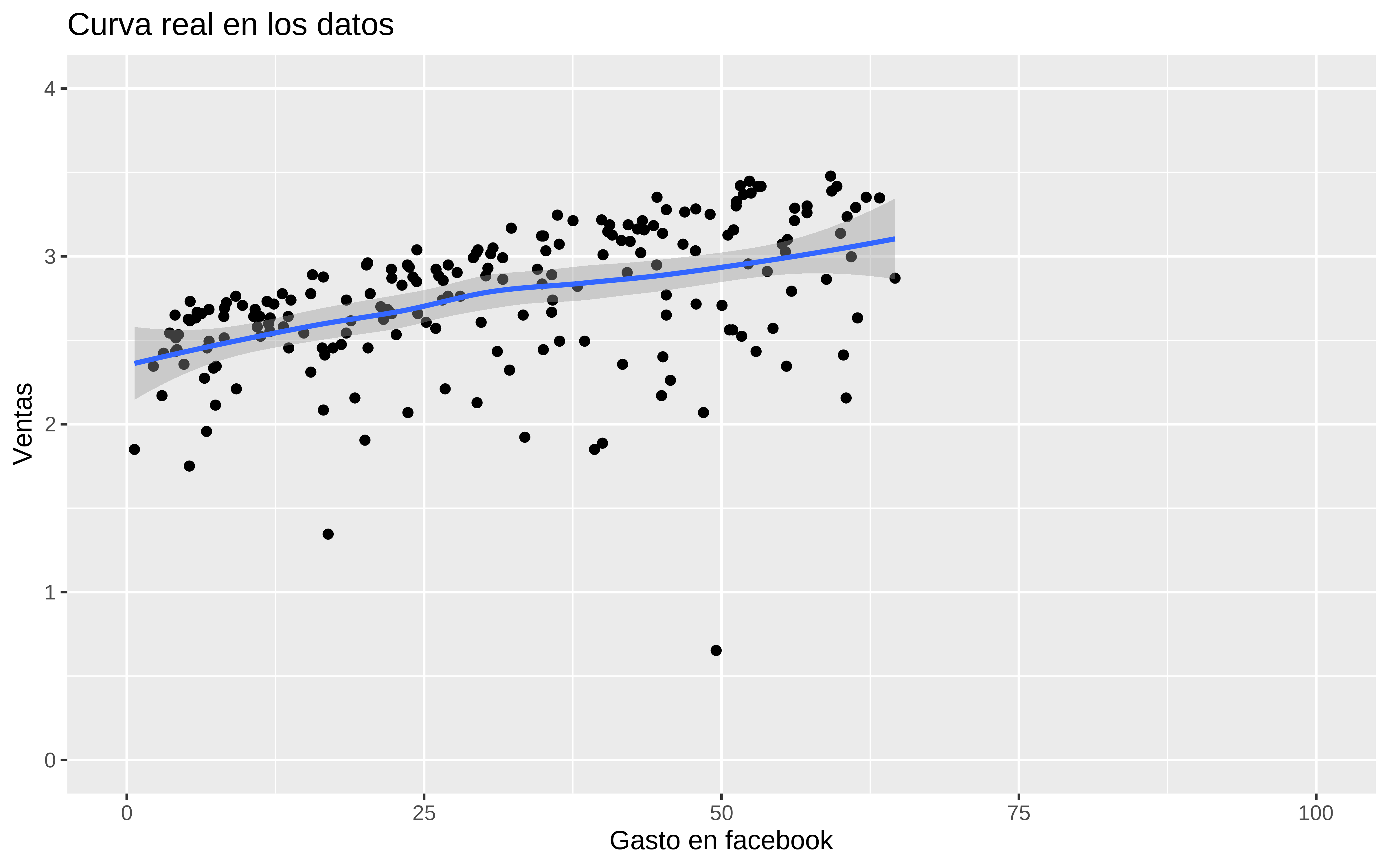

Mas teoría marketiniana

Una forma de modelar la curva de saturación que tienen los de marketing es utilizar la saturación de Hill, que viene de la bioquímica y ámbitos similares. Y bueno, tal y como dice Richard McElreath, “ciencia antes que estadística” y quién soy yo para refutar que se use lo de las curvas de saturación de Hill.

Podemos considerar algo como esto pero para cada canal \[ \text{log(ventas)} = \dfrac{\beta \cdot \text{adstock}^{h}}{S^h + \text{adstock}^h} \]

Por lo que tendríamos para cada canal un parámetro \(\beta\) un parámetro \(h\) y un parámetro \(S\) .

Esta función no es lineal en los parámetros, pero podemos definir el modelo generativo y ajustar a los datos usando MCMC

# como no me deja poner splines meto un coeficiente al tiempo. 

hill_adstock_formula <- bf(
  log(sales) ~ bintercept + bfb * ads_fb ^ hfb  / (Sfb^hfb + ads_fb ^ hfb)  +
    byoutube * ads_youtube ^ hyou / (Syoutube^hyou + ads_youtube ^ hyou) +
    bnews * ads_news ^ hnews / (Snews^hnews + ads_news ^ hnews) + btime * time, 
  bfb + Sfb + byoutube + Syoutube + bnews + Snews + btime + hfb + hyou + hnews ~ 1,
  nl = TRUE
)
# Define los priors para los parámetros del modelo

priors <- c(
  prior(normal(0, 10), nlpar = "bintercept"),
  prior(normal(0, 10), nlpar = "bfb", lb = 0),
  prior(normal(0, 10), nlpar = "Sfb"),
  prior(normal(0, 10), nlpar = "byoutube", lb = 0 ),
  prior(normal(0, 50), nlpar = "Syoutube"),
  prior(normal(0, 50), nlpar = "bnews", lb = -0.1),
  prior(normal(0, 50), nlpar = "Snews"),
  prior(normal(0, 50), nlpar = "btime", lb = 0),
  prior(lognormal(log(1), 0.5), nlpar = "hfb", lb = 0),
  prior(lognormal(log(1), 0.5), nlpar = "hyou", lb = 0),
  prior(lognormal(log(1), 0.5), nlpar = "hnews", lb = 0)
)



# Ajusta el modelo con brms pero con más iteraciones,

modelo_hill_adstock <- brm(
  formula = hill_adstock_formula,
  data = datos,
  family = gaussian(),
  prior = priors,
  chains = 4, iter = 6000, warmup = 1000, 
  control = list( adapt_delta = 0.97),
  backend = "cmdstanr",cores = 4, file = here::here("2024/06/mod_hill") 
)

Algunos chequeos del modelo

Como antes, comparamos la distribucion de las ventas con las generadas por el modelo.

# Muestra un resumen del modelo
summary(modelo_hill_adstock)
#>  Family: gaussian 
#>   Links: mu = identity; sigma = identity 
#> Formula: log(sales) ~ bfb * ads_fb^hfb/(Sfb^hfb + ads_fb^hfb) + byoutube * ads_youtube^hyou/(Syoutube^hyou + ads_youtube^hyou) + bnews * ads_news^hnews/(Snews^hnews + ads_news^hnews) + btime * time 
#>          bfb ~ 1
#>          Sfb ~ 1
#>          byoutube ~ 1
#>          Syoutube ~ 1
#>          bnews ~ 1
#>          Snews ~ 1
#>          btime ~ 1
#>          hfb ~ 1
#>          hyou ~ 1
#>          hnews ~ 1
#>    Data: datos (Number of observations: 200) 
#>   Draws: 4 chains, each with iter = 6000; warmup = 1000; thin = 1;
#>          total post-warmup draws = 20000
#> 
#> Regression Coefficients:
#>                    Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> bfb_Intercept          0.69      0.09     0.54     0.88 1.00     2575     2820
#> Sfb_Intercept         34.66      3.59    28.77    42.91 1.00     2990     2447
#> byoutube_Intercept     3.20      0.13     2.99     3.49 1.00     1669     1572
#> Syoutube_Intercept    37.05      3.28    32.19    45.05 1.00     1913     1567
#> bnews_Intercept       -0.01      0.06    -0.10     0.14 1.00     2447     2365
#> Snews_Intercept       38.65     31.64     1.38   114.80 1.00     2133     3496
#> btime_Intercept        0.00      0.00     0.00     0.00 1.00     3306     2238
#> hfb_Intercept          2.62      0.44     1.89     3.61 1.00     3007     4464
#> hyou_Intercept         0.84      0.08     0.67     1.01 1.00     1719     1662
#> hnews_Intercept        1.06      0.57     0.34     2.52 1.00     4290     4024
#> 
#> Further Distributional Parameters:
#>       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sigma     0.13      0.01     0.12     0.14 1.00     4955     6336
#> 
#> Draws were sampled using sample(hmc). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).
pp_check(modelo_hill_adstock, ndraws = 100)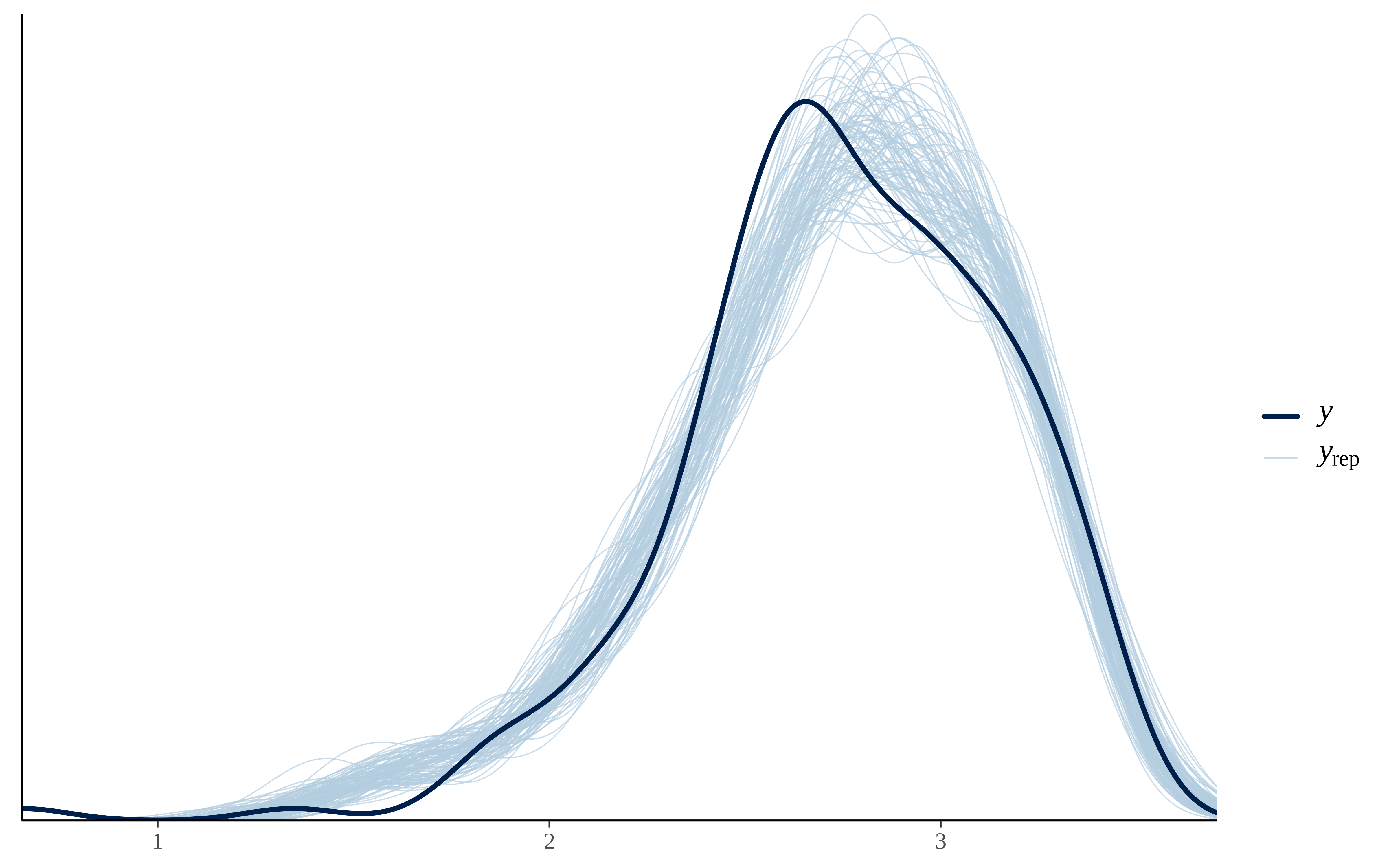

Aunque tengo que leer a Carlos sobre el tema de Leave One Out, es una cosa que se utiliza bastante en validación de modelos bayesianos, debido al trabajo de Aki Vehtari, Gelman y Gabry en este campo , ver aquí

El Pareto k diagnostic nos indica que sólo hay problemas con un dato, así que tampoco nos vamos a preocupar mucho.

loo(modelo_hill_adstock)
#> 
#> Computed from 20000 by 200 log-likelihood matrix.
#> 
#>          Estimate   SE
#> elpd_loo    114.0 41.6
#> p_loo        25.6 17.7
#> looic      -228.0 83.3
#> ------
#> MCSE of elpd_loo is NA.
#> MCSE and ESS estimates assume MCMC draws (r_eff in [0.1, 0.6]).
#> 
#> Pareto k diagnostic values:
#>                          Count Pct.    Min. ESS
#> (-Inf, 0.7]   (good)     199   99.5%   1122    
#>    (0.7, 1]   (bad)        0    0.0%   <NA>    
#>    (1, Inf)   (very bad)   1    0.5%   <NA>    
#> See help('pareto-k-diagnostic') for details.

Veamos que tal predice en test

pred_test <-  posterior_predict(modelo_hill_adstock, newdata = test)

test$ventas_predichas_mod_hill  <- exp(apply(pred_test, 2, mean))

yardstick::rmse(test,sales, ventas_predichas_mod_hill)
#> # A tibble: 1 × 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        1.42
yardstick::mae(test,sales, ventas_predichas_mod_hill)
#> # A tibble: 1 × 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 mae     standard        1.08

Que es mejor predicción que el modelo simple original

# rmse y mae con modelo simple
yardstick::rmse(test,sales, ventas_predichas)
#> # A tibble: 1 × 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 rmse    standard        2.45
yardstick::mae(test,sales, ventas_predichas)
#> # A tibble: 1 × 3
#>   .metric .estimator .estimate
#>   <chr>   <chr>          <dbl>
#> 1 mae     standard        1.91

Usamos el modelo para obtener predicciones al global de los datos, train y test

predicciones <- posterior_predict(modelo_hill_adstock, newdata = datos, ndraws = 1000) 

# Calcular las predicciones medias
predicciones_medias <- apply(predicciones, 2, mean)

# Agregar las predicciones al dataframe de nuevos datos
datos$ventas_predichas <- exp(predicciones_medias)


# Curva de saturación para publicidad

p_youtube_estimada <- datos %>% 
  group_by(ads_youtube) %>%
  summarise(ventas_predichas_mean = median(ventas_predichas),
            low = quantile(ventas_predichas, 0.05), 
            high = quantile(ventas_predichas, 0.95)) %>%
  ggplot(aes(x = ads_youtube, y = ventas_predichas_mean)) +
  geom_line() +
  geom_ribbon(aes(ymin = low, ymax = high), alpha = 0.3) +
  labs(title = "Curva de Saturación para Youtube",
       x = "Gasto en Youtube",
       y = "Ventas Predichas")
p_youtube_estimada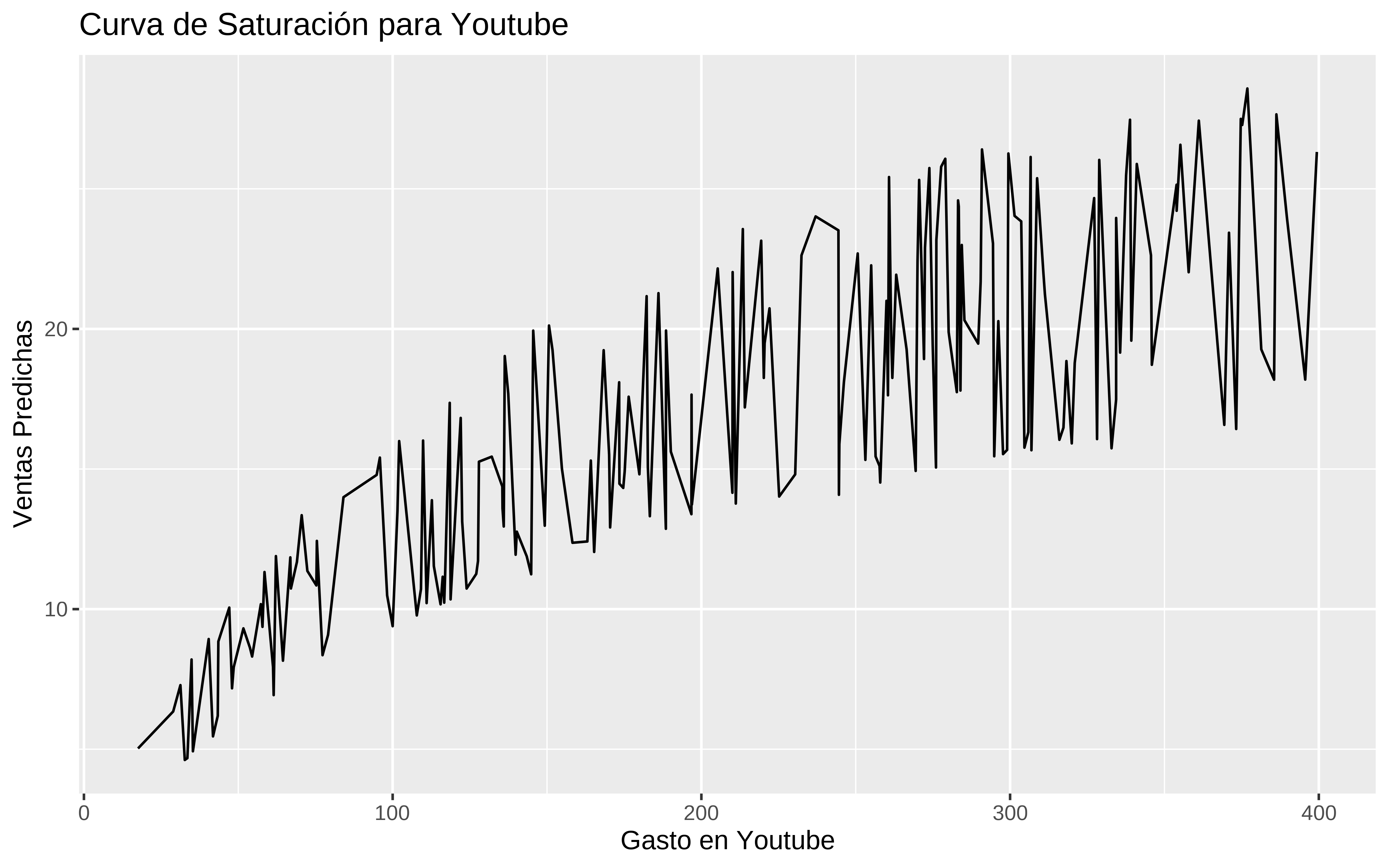

Y esta curva tiene muchos picos, porque en el conjunto de datos original no están todas las posibles combinaciones entre las diferentes inversiones en los canales.

Curva de saturación usando un conjunto de datos sintético

Podríamos obtener las curvas de saturación marginalizando la inversión en un canal, teniendo en cuenta muchas posibles combinaciones de inversiones en los otros canales. Esta sería una forma de aproximarse a la curva de saturación, aunque el volumen de ventas que sale estará sobreestimado, puesto que es un dataset sintético, dónde están sobre-representadas combinaciones de inversiones con valores mucho más altos que los observados en los datos.

# Crear un rango de valores para publicidad y promociones
ads_fb <- seq(0, 400, length.out = 30)
ads_youtube <- seq(0, 400, length.out = 30)
ads_news <- seq(0, 400, length.out = 30)
time <-  rep(201, 30)

# Crear un nuevo dataframe para predicciones
nuevos_datos <- expand.grid(
  ads_fb = ads_fb,
  ads_youtube = ads_youtube,
  ads_news = ads_news,
  time = time
) 
head(nuevos_datos)
#>     ads_fb ads_youtube ads_news time
#> 1  0.00000           0        0  201
#> 2 13.79310           0        0  201
#> 3 27.58621           0        0  201
#> 4 41.37931           0        0  201
#> 5 55.17241           0        0  201
#> 6 68.96552           0        0  201
# son demasiados datos , tomo una muestra, que no es pecado
dim(nuevos_datos)
#> [1] 810000      4

Combinar todo con todo nos da más de 800 mil filas, lo cual es excesivo. Así que, tal y como se llama este blog, muestrear no es pecado, tomamos una muestra de estos datos sintéticos que también nos vale.

nuevos_datos <-  nuevos_datos %>% 
  sample_n(4000)

predicciones <- posterior_predict(modelo_hill_adstock, newdata = nuevos_datos, ndraws = 1000) 

# Calcular las predicciones medias

# Agregar las predicciones, en log de ventas,  al dataframe de nuevos datos
nuevos_datos$ventas_predichas <- apply(predicciones, 2, mean)

# Curva de saturación para publicidad

p_youtube_estimada_bis <- nuevos_datos %>% 
  group_by(ads_youtube) %>%
  summarise(ventas_predichas_mean = median(ventas_predichas),
            low = quantile(ventas_predichas, 0.05), 
            high = quantile(ventas_predichas, 0.95)) %>%
  ggplot(aes(x = ads_youtube, y = ventas_predichas_mean)) +
  geom_line() +
  geom_ribbon(aes(ymin = low, ymax = high), alpha = 0.2)+ 
  labs(title = "Curva de Saturación para Youtube",
       x = "Gasto en Youtube",
       y = "Ventas Predichas")
library(patchwork)
p_youtube_real + p_youtube_estimada_bis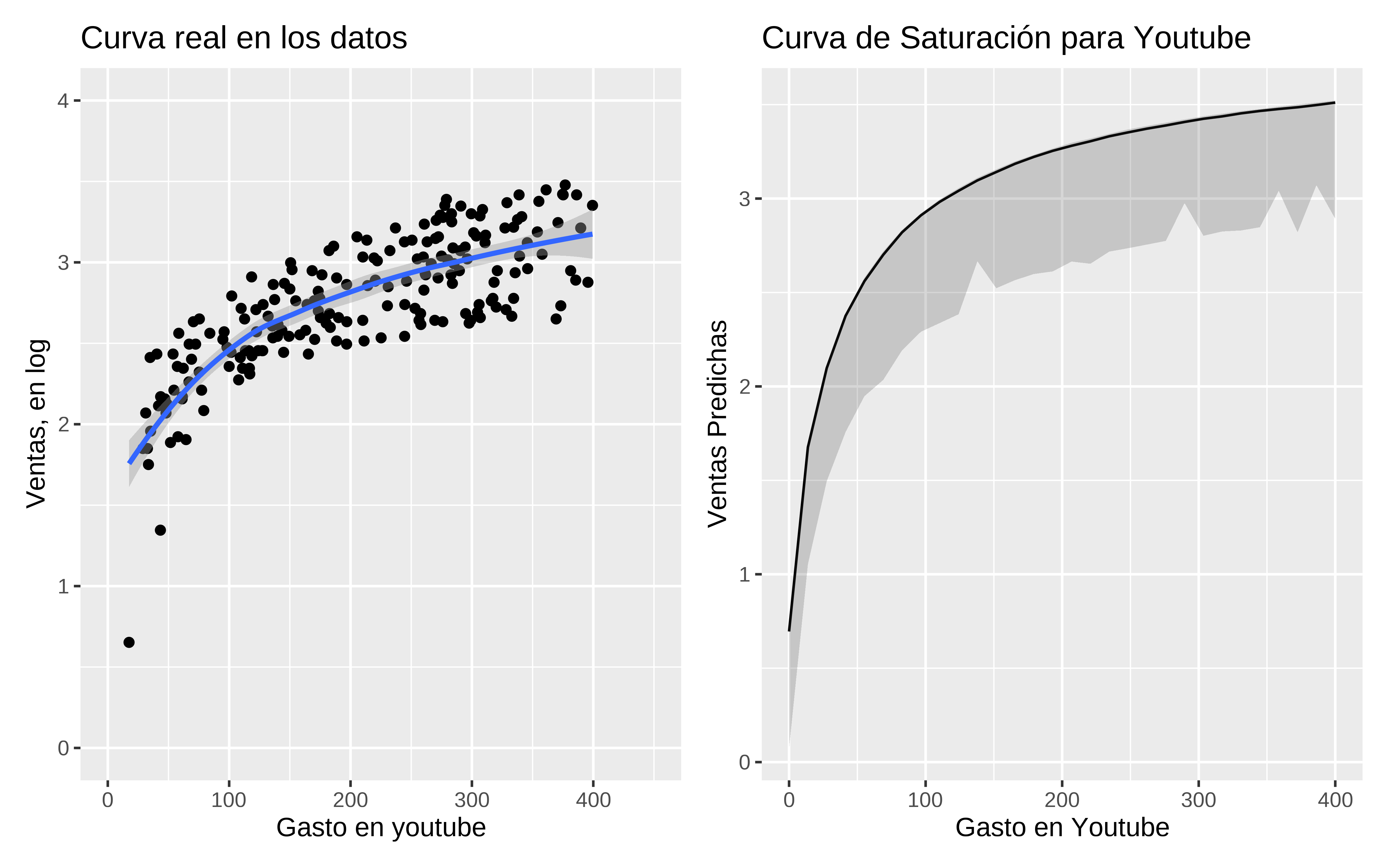

Última optimización

No faltaría más que optimizar la inversión publicitaria que nos saldría con este modelo, y manteniendo mismo presupuesto

f_objetivo_partial_nueva  <- partial(funcion_objetivo, modelo = modelo_hill_adstock, presupuesto = 500)
f_objetivo_partial_nueva
#> <partialised>
#> function (...) 
#> funcion_objetivo(modelo = modelo_hill_adstock, presupuesto = 500, 
#>     ...)

# exporto el modelo y la funcion objetivo a los procesos en paralelo

clusterExport(cl,c('f_objetivo_partial_nueva', 'modelo_hill_adstock'))

Optimizamos

bayes_opt_nueva <- bayesOpt(
  FUN = f_objetivo_partial_nueva,
  bounds = bounds,
  initPoints = 10,
  acq = "ei",
  iters.n = 200,
  iters.k = 10,
  kappa = 2,
  eps = 0.0, 
  parallel = TRUE,
  otherHalting = list(timeLimit = 300)
)

Y al igual que antes obtenemos los resultados de la optimización

print(bayes_opt_nueva)
#> Class: bayesOpt
#> 
#>                     Epochs: 14
#>                 Iterations: 166
#>        Average FUN Seconds: 1
#>        Highest FUN Seconds: 1.18
#> Final Expected Improvement: 1.661111e-218
#>                 GP Updated: TRUE
#>                Stop Status: Stopped Early. See $stopStatus
bayes_opt_nueva$scoreSummary %>% 
  arrange(Score) 
#>      Epoch Iteration facebook_new youtube_new news_new     gpUtility acqOptimum
#>      <num>     <int>        <num>       <num>    <num>         <num>     <lgcl>
#>   1:     0        10     99.65962    363.3601 22.38239            NA      FALSE
#>   2:    13       155    186.81997    276.0443 30.76712  0.000000e+00      FALSE
#>   3:    13       154    199.64561    263.3377 31.71919 3.200023e-316      FALSE
#>   4:    13       156    210.76776    251.6358 34.00000 4.741560e-231      FALSE
#>   5:    13       147    202.50964    249.9072 32.76780 2.121759e-281       TRUE
#>  ---                                                                           
#> 162:     3        38    218.94138    395.4012 32.60496  3.226181e-01      FALSE
#> 163:     3        39    215.57359    400.0000 31.55908  3.330606e-01      FALSE
#> 164:     3        36    215.06796    398.3064 34.00000  3.369026e-01      FALSE
#> 165:     3        34    224.00000    400.0000 33.15132  4.906921e-01      FALSE
#> 166:     3        31    224.00000    400.0000 34.00000  5.049163e-01       TRUE
#>      inBounds Elapsed         Score errorMessage
#>        <lgcl>   <num>         <num>       <lgcl>
#>   1:     TRUE   1.011 -3.446360e+00           NA
#>   2:     TRUE   0.928 -3.393987e+00           NA
#>   3:     TRUE   0.952 -3.383473e+00           NA
#>   4:     TRUE   0.956 -3.373160e+00           NA
#>   5:     TRUE   1.036 -3.360140e+00           NA
#>  ---                                            
#> 162:     TRUE   0.930  2.159359e+10           NA
#> 163:     TRUE   0.932  2.164802e+10           NA
#> 164:     TRUE   0.984  2.171920e+10           NA
#> 165:     TRUE   1.006  2.469654e+10           NA
#> 166:     TRUE   0.948  2.496400e+10           NA

Comprobamos que se cumple la restricción de presupuesto

(result_bayes_nueva <- bayes_opt_nueva$scoreSummary %>% 
 arrange(Score) %>% 
 head(1) %>% 
 select(facebook_new, youtube_new, news_new) )
#>    facebook_new youtube_new news_new
#>           <num>       <num>    <num>
#> 1:     99.65962    363.3601 22.38239

Vemos que la optimización es diferente, el modelo simple no tenía modelada la saturación da mucho más inversión en facebook que el modelo con saturación.

result_bayes %>% select(facebook_new, youtube_new, news_new)
#>    facebook_new youtube_new news_new
#>           <num>       <num>    <num>
#> 1:     202.9549    176.0488 15.10575

Comprobamos que no se ha pasado del presupuesto

with(result_bayes_nueva, sum(facebook_new, youtube_new, news_new))
#> [1] 485.4021

Simulamos las ventas que se esperan con esta optimización.

simulaciones_optim_nueva <- simular_ventas_siguiente_periodo(result_bayes_nueva$facebook_new, result_bayes_nueva$youtube_new, result_bayes$news_new,
                                                       modelo = modelo_hill_adstock)
exp(quantile(simulaciones_optim_nueva, c(0.2, 0.5, 0.8)))
#>      20%      50%      80% 
#> 27.91540 31.31265 34.85574

(p_optim_hill <- simulaciones_optim_nueva %>% 
  as_tibble() %>% 
  ggplot(aes(x = exp(value))) +
  geom_density() +
  labs(title = "Distribución de ventas esperadas tras optimización",
       subtitle = "Modelo con saturación de Hill",
       x = "Ventas esperadas",
       y = "Densidad") +
  theme_minimal())

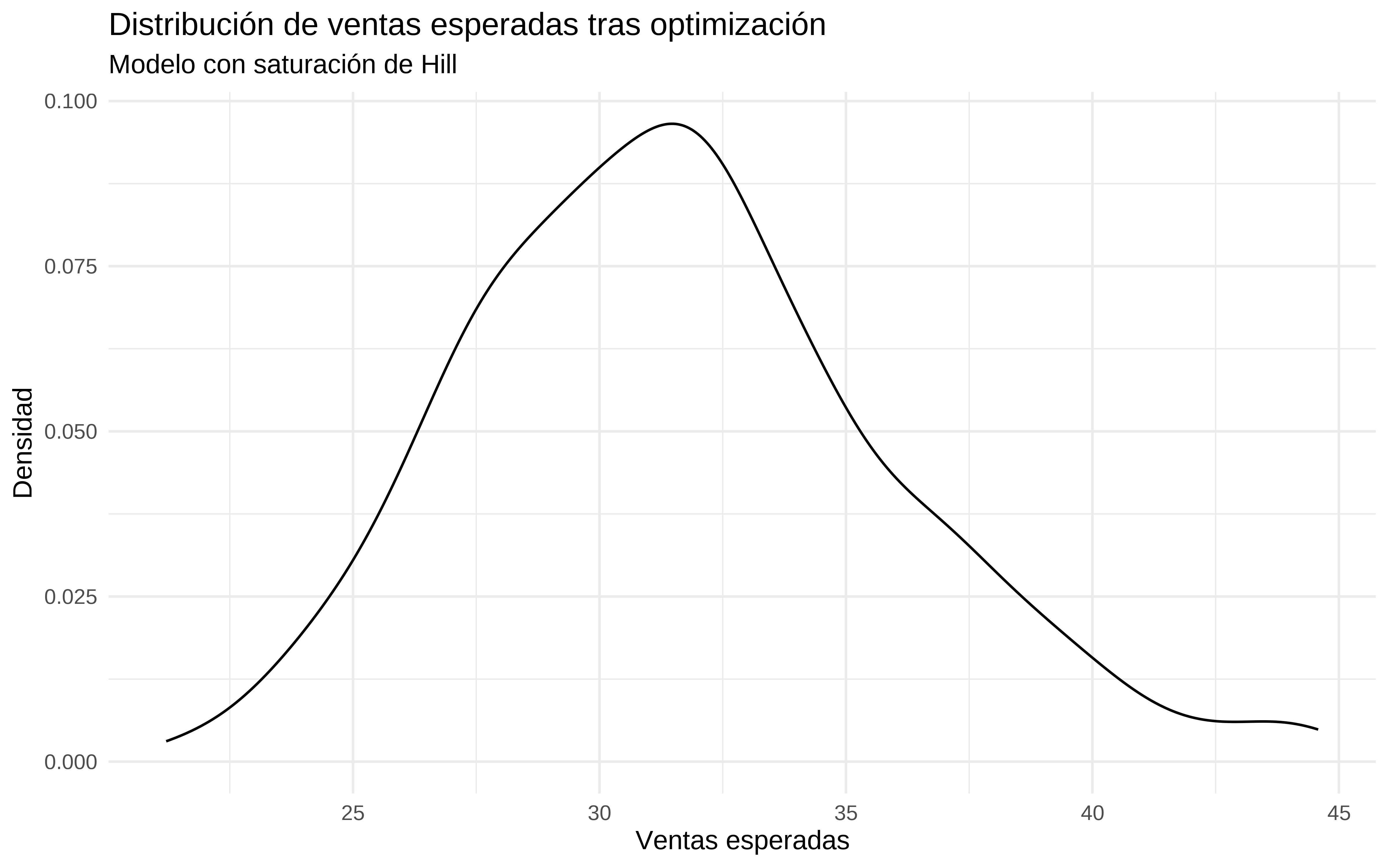
A nivel de ventas estimadas, me resulta más creíble la que devuelve el modelo con saturación. El modelo más simple extrapola demasiado. Al fin y al cabo modelar la saturación es “equivalente” a restringir los coeficientes.

p_optimizacion_mod_spline  + p_optim_hill